

分析 (1)由管中放置同样的绳子AA1、BB1、CC1,直接利用概率公式求解即可求得答案;
(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与这三根绳子能连结成一根长绳的情况,再利用概率公式即可求得答案.
解答 解:(1)∵管中放置同样的绳子AA1、BB1、CC1,
∴小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是:$\frac{1}{3}$;
故答案为:$\frac{1}{3}$;
(2)列表得:
| 右端 左端 | A1B1 | B1C1 | A1C1 |
| AB | AB,A1B1 | AB,B1C1 | AB,A1C1 |
| BC | BC,A1B1 | BC,B1C1 | BC,A1C1 |
| AC | AC,A1B1 | AC,B1C1 | AC,A1C1 |
点评 此题考查了列表法或树状图法求概率.注意首先分别求得左右两端的情况,再列表是关键.用到的知识点为:概率=所求情况数与总情况数之比.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
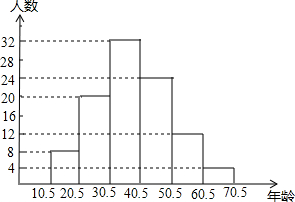 今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:
今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
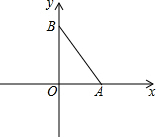 如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).
如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为(3,4)或($\frac{96}{25}$,$\frac{72}{25}$)或(-$\frac{21}{25}$,$\frac{28}{25}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
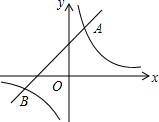 如图,已知在平面直角坐标系中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上.一次函数y=x+b的图象过点A,且与反比例函数图象的另一交点为B.
如图,已知在平面直角坐标系中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上.一次函数y=x+b的图象过点A,且与反比例函数图象的另一交点为B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com