
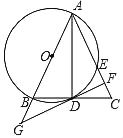
【题目】如图,△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于点E,过点D作DF⊥AC于点F,交AB延长线于点G,连结AD.
(1)∠ADB= °,依据是 ;
(2)求证:DF是圆O的切线;
(3)已知BC=4![]() ,CF=2,求AE和BG的长.
,CF=2,求AE和BG的长.
【答案】(1)90,半圆(或直径)所对的圆周角是直角;(2)见解析;(3)AE=6,BG=![]() .
.
【解析】
(1)根据半圆(或直径)所对的圆周角是直角可得结论;
(2)连接OD,由(1)知AD⊥BC,结合等腰三角形的性质知BD=CD,再根据OA=OB知OD∥AC,从而由DF⊥AC可得OD⊥DF,即可得证;
(3)连接BE.BE∥DF,可得DF是△BEC的中位线,设AE=x,则AC=AB=x+4,根据勾股定理列方程可得x的值,证明△GOD∽△GAF,列比例式可得BG的长.
解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
故答案为:90,半圆(或直径)所对的圆周角是直角;
(2)连接OD,
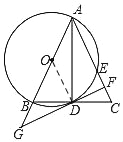
∵∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
又∵OA=OB,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是圆O的切线;
(3)连接BE.
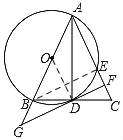
∵CD=![]() BC=2
BC=2![]() ,
,
∵CF=2,
∴DF=![]() =
=![]() =4,
=4,
∵AB是直径,
∴∠AEB=∠CEB=90°,
∴BE⊥AC,
∵DF⊥AC,
∴DF∥BE,
∴EF=FC=2,
∴BE=2DF=8,
设AE=x,则AC=AB=x+4
由勾股定理得:AB2=AE2+BE2,
(x+4)2=82+x2,
x=6,
∴AE=6,AB=4+6=10,
∵OD∥AF,
∴△GOD∽△GAF,
∴![]() ,
,
∴![]() ,BG=
,BG=![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同。
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率。(请利用树状图或列表法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
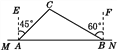
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
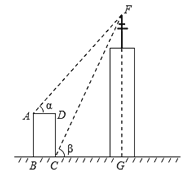
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°,矩形建筑物宽度AD=20m,高度CD=30m,则信号发射塔顶端到地面的高度FG为__米(结果精确到1m).
参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,cos65°=0.4,tan65°=2.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=(x-2)2+m与x轴交于点A和B,与y轴交于点C,点D是点C关于抛物线对称轴的对称点,若点A的坐标为(1,0),直线y2=kx+b经过点A,D.
(1)求抛物线的函数解析式;
(2)求点D的坐标和直线AD的函数解析式;
(3)根据图象指出,当x取何值时,y2>y1.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com