
،¾جâؤ؟،؟بçح¼£¬شع³¤·½ذخ![]() ضذ£¬
ضذ£¬![]() cm£¬
cm£¬![]() cm£¬µم
cm£¬µم![]() خھ
خھ![]() µؤضذµم.بôµم
µؤضذµم.بôµم![]() شعدك¶خ
شعدك¶خ![]() ةدزش1 cm/sµؤثظ¶بسةµم
ةدزش1 cm/sµؤثظ¶بسةµم![]() دٍµم
دٍµم![]() شث¶¯£¬µ½µم
شث¶¯£¬µ½µم![]() ت±²»¶¯.ح¬ت±£¬µم
ت±²»¶¯.ح¬ت±£¬µم![]() شعدك¶خ
شعدك¶خ![]() ةدسةµم
ةدسةµم![]() دٍµم
دٍµم![]() شث¶¯.
شث¶¯.
(1)بôµم![]() µؤشث¶¯ثظ¶بسëµم
µؤشث¶¯ثظ¶بسëµم![]() µؤشث¶¯ثظ¶بدàµب£¬¾¹1 s؛َ£¬
µؤشث¶¯ثظ¶بدàµب£¬¾¹1 s؛َ£¬![]() سë
سë![]() تا·ٌب«µب?اëثµأ÷ہيسة£¬²¢إذ¶د´ثت±دك¶خ
تا·ٌب«µب?اëثµأ÷ہيسة£¬²¢إذ¶د´ثت±دك¶خ![]() ؛ح
؛ح![]() µؤخ»ضأ¹طدµ;
µؤخ»ضأ¹طدµ;
(2)بôµم![]() µؤشث¶¯ثظ¶بسëµم
µؤشث¶¯ثظ¶بسëµم![]() µؤشث¶¯ثظ¶بدàµب£¬شث¶¯ت±¼نخھ
µؤشث¶¯ثظ¶بدàµب£¬شث¶¯ت±¼نخھ![]() s£¬ةè
s£¬ةè![]() µؤأو»خھ
µؤأو»خھ![]() cm2£¬اëسأ؛¬
cm2£¬اëسأ؛¬![]() µؤ´ْتت½±يت¾
µؤ´ْتت½±يت¾
(3)بôµم![]() µؤشث¶¯ثظ¶بسëµم
µؤشث¶¯ثظ¶بسëµم![]() µؤشث¶¯ثظ¶ب²»دàµب£¬µ±µم
µؤشث¶¯ثظ¶ب²»دàµب£¬µ±µم![]() µؤشث¶¯ثظ¶بخھ¶àةظت±£¬ؤـ¹»ت¹
µؤشث¶¯ثظ¶بخھ¶àةظت±£¬ؤـ¹»ت¹![]() سë
سë![]() ب«µب?
ب«µب?
،¾´ً°¸،؟£¨1£©¼û½âخِ£»£¨2£©S=![]()
![]() t+6;£¨3£©
t+6;£¨3£©![]() cm/s
cm/s
،¾½âخِ،؟
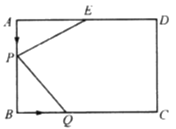
£¨1£©±¾جâ؛ـبفز×ض¤أ÷،÷AEP،ص،÷BPQ£¬صâرù؟ةµأ³ِ،دAEP=،دBPQ£¬زٍخھ،دAEP+،دAPE=90،م£¬؟ةµأ³ِ،دBPQ+،دAPE=90،م£¬صâ¼´؟ةإذ¶د³ِ½لآغ£®
£¨2£©؟ة·ض±ًسأt±يت¾³ِAP،¢BQ،¢BP،¢CQµؤ³¤¶ب£¬ب»؛َسأ¾طذخµؤأو»¼ُب¥،÷APE،¢،÷BPQ¼°جفذخEDCQµؤأو»¼´؟ةµأ³ِ،÷PEQµؤأو»خھScm2£®
£¨3£©ةèQشث¶¯µؤثظ¶بخھxcm/s£¬شٍ¸ù¾ف،÷AEPسë،÷BQPµأ³ِAP=BP،¢AE=BQ»ٍAP=BQ£¬AE=BP£¬´س¶ّ؟ةءذ³ِ·½³ج×飬½â³ِ¼´؟ةµأ³ِ´ً°¸£®
(1)،ك³¤·½ذخABCD £¬
£¬
،à،دA=،دB=90،م£¬
،كµمEخھADµؤضذµم£¬AD=6cm£¬
،àAE=3cm£¬
سض،كP؛حQµؤثظ¶بدàµب؟ةµأ³ِAP=BQ=1cm£¬BP=3£¬
،àAE=BP£¬
شع،÷AEP؛ح،÷BQPضذ£¬
 £¬
£¬
،à،÷AEP،ص،÷BPQ£¬
،à،دAEP=،دBPQ£¬
سض،ك،دAEP+،دAPE=90،م£¬
¹ت؟ةµأ³ِ،دBPQ+،دAPE=90،م,¼´،دEPQ=90،م£¬
¼´EP،حPQ.
(2)ء¬½سQE,سةجâزâµأ£؛AP=BQ=t,BP=4t,CQ=6t,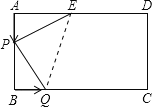
SPEQ=SABCDSBPQSEDCQSAPE=AD،ءAB![]() AE،ءAP
AE،ءAP![]() BP،ءBQ
BP،ءBQ![]() (DE+CQ)،ءCD=24
(DE+CQ)،ءCD=24![]() ،ء3t
،ء3t![]() t(4t)
t(4t) ![]() ،ء4(3+6t)=
،ء4(3+6t)= ![]()
![]() t+6£¬
t+6£¬
(3)ةèµمQµؤشث¶¯ثظ¶بخھxcm/s£¬
¢ظ¾¹yأë؛َ,،÷AEP،ص،÷BQP£¬شٍAP=BP£¬AE=BQ£¬
،à![]() £¬
£¬
½âµأ£؛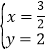 £¬
£¬
¼´µمQµؤشث¶¯ثظ¶بخھ![]() cm/sت±ؤـت¹ء½ب½اذخب«µب.
cm/sت±ؤـت¹ء½ب½اذخب«µب.![]()
¢ع¾¹yأë؛َ,،÷AEP،ص،÷BPQ£¬شٍAP=BQ£¬AE=BP£¬
،ày=xy,3=4y£¬
½âµأ£؛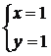 (ةلب¥).
(ةلب¥).
×غةدثùتِ,µمQµؤشث¶¯ثظ¶بخھ![]() cm/sت±ؤـت¹ء½ب½اذخب«µب،£
cm/sت±ؤـت¹ء½ب½اذخب«µب،£


 الثة¶ل¹عب«ؤـصئ؟ط¾يدµءذ´ً°¸
الثة¶ل¹عب«ؤـصئ؟ط¾يدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعRt،÷ABCضذ£¬،دACB=90،م£¬زشµمAخھش²ذؤ£¬ACخھ°ë¾¶£¬×÷،رA½»ABسعµمD£¬½»CAµؤرس³¤دكسعµمE£¬¹µمE×÷ABµؤئ½ذذدكEF½»،رAسعµمF£¬ء¬½سAF،¢BF£¬DF£®
£¨1£©اَض¤£؛BF،حAF£»
£¨2£©µ±،دCABµبسع¶àةظ¶بت±£¬ثؤ±كذخADEFخھءâذخ£؟اë¸ّسèض¤أ÷£® 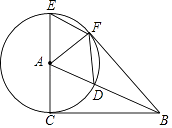
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟(1)ةè![]() بô
بô![]() اَA-2Bµؤضµ£»
اَA-2Bµؤضµ£»
(2)ؤ³¹«ث¾سذ¼×،¢ززء½ہà¾سھتصبë,ب¥ؤê¼×ہàتصبëتاززہàتصبëµؤ2±¶,ش¤¼ئ½ٌؤê¼×ہàؤêتصبë¼ُةظ9%,ززہàتصب뽫شِ¼س19%،£خت½ٌؤê¸أ¹«ث¾µؤؤê×ـتصبë±بب¥ؤêشِ¼سءثآً?اëثµأ÷ہيسة،£
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟4شآ23بصتا،°تہ½ç¶ءتéبص،±£¬ر§ذ£؟ھص¹،°بأتéدمزçآْذ£ش°،±¶ءتé»î¶¯£¬زشجلةاàةظؤêµؤشؤ¶ءذثب¤£¬¾إؤ꼶£¨1£©°àتر§»î¶¯ذ،×é¶ش±¾ؤ꼶600أûر§ةْأ؟جىشؤ¶ءت±¼ن½ّذذءثح³¼ئ£¬¸ù¾فثùµأت¾ف»وضئءثء½·ù²»حêصûح³¼ئح¼£¨أ؟×é°üہ¨×îذ،ضµ²»°üہ¨×î´َضµ£©.¾إؤ꼶£¨1£©°àأ؟جىشؤ¶ءت±¼نشع0.5ذ،ت±زشؤعµؤر§ةْص¼ب«°àبثتµؤ8%.¸ù¾فح³¼ئح¼½â´ًدآءذختجâ£؛
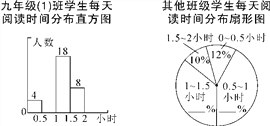
£¨1£©¾إؤ꼶£¨1£©°àسذ،،،،،،،،أûر§ةْ£»
£¨2£©²¹ب«ض±·½ح¼£»
£¨3£©³¾إؤ꼶£¨1£©°àح⣬¾إؤ꼶ئنثû°à¼¶أ؟جىشؤ¶ءت±¼نشع1،«1.5ذ،ت±µؤر§ةْسذ165بث£¬اëؤم²¹ب«ةبذخح³¼ئح¼£»
£¨4£©اَ¸أؤ꼶أ؟جىشؤ¶ءت±¼ن²»ةظسع1ذ،ت±µؤر§ةْسذ¶àةظبث.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
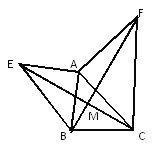
،¾جâؤ؟،؟بçح¼ثùت¾£¬زرضھAE،حAB£¬AF،حAC£¬AE=AB£¬AF=AC.اَض¤£؛£¨1£©EC=BF£»£¨2£©EC،حBF.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟£¨1£©ختجâ±³¾°£؛
بçح¼1£¬شعثؤ±كذخABCDضذ£¬AB£½AD£¬،دBAD£½120،م£¬،دB£½،دADC£½90،م£¬E،¢F·ض±ًتاBC£¬CDةدµؤµم£¬از،دEAF£½60،م£¬ج½¾؟ح¼ضذدك¶خBE£¬EF£¬FDض®¼نµؤتء؟¹طدµ£®
ذ،حُح¬ر§ج½¾؟´ثختجâµؤ·½·¨تارس³¤FDµ½µمG£¬ت¹DG£½BE£¬ء¬½لAG£¬دبض¤أ÷،÷ABE،ص،÷ADG£¬شظض¤أ÷،÷AEF،ص،÷AGF£¬؟ةµأ³ِ½لآغ£¬ثûµؤ½لآغس¦تا £»

£¨2£©ج½ث÷رسةى£؛
بçح¼2£¬بôشعثؤ±كذخABCDضذ£¬AB£½AD£¬،دB£«،دD£½180،م£¬E£¬F·ض±ًتاBC£¬CDةدµؤµم£¬از،دEAF£½![]() ،دBAD£¬ةدتِ½لآغتا·ٌبشب»³ةء¢£¬²¢ثµأ÷ہيسة£»
،دBAD£¬ةدتِ½لآغتا·ٌبشب»³ةء¢£¬²¢ثµأ÷ہيسة£»
£¨3£©½لآغس¦سأ£؛
بçح¼3£¬شعؤ³´خ¾üتآرفد°ضذ£¬½¢ح§¼×شعض¸»سضذذؤ£¨O´¦£©±±ئ«خ÷30،مµؤA´¦£¬½¢ح§ززشعض¸»سضذذؤؤدئ«¶«70،مµؤB´¦£¬²¢ازء½½¢ح§µ½ض¸»سضذذؤµؤ¾àہëدàµب£®½سµ½ذذ¶¯ض¸ءî؛َ£¬½¢ح§¼×دٍص¶«·½دٍزش60؛£ہï/ذ،ت±µؤثظ¶با°½ّ£¬½¢ح§ززرط±±ئ«¶«50،مµؤ·½دٍزش80؛£ہï/ذ،ت±µؤثظ¶با°½ّ£¬1.5ذ،ت±؛َ£¬ض¸»سضذذؤ¹غ²âµ½¼×،¢ززء½½¢ح§·ض±ًµ½´ïE£¬F´¦£¬ازء½½¢ح§سëض¸»سضذذؤOض®¼ن¼ذ½ا،دEOF=70،م£¬تشاَ´ثت±ء½½¢ح§ض®¼نµؤ¾àہ룮
£¨4£©ؤـء¦جل¸ك£؛
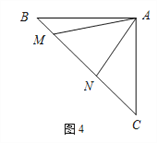
بçح¼4£¬µبرüض±½اب½اذخABCضذ£¬،دBAC£½90،م£¬AB£½AC£¬µمM£¬Nشع±كBCةد£¬از،دMAN£½45،م£®بôBM£½1£¬CN£½3£¬تشاَ³ِMNµؤ³¤£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟،¾ج½¾؟؛¯تy=x+ ![]() µؤح¼دَسëذشضت،؟
µؤح¼دَسëذشضت،؟
£¨1£©؛¯تy=x+ ![]() µؤ×ش±نء؟xµؤب،ضµ·¶خ§تا£»
µؤ×ش±نء؟xµؤب،ضµ·¶خ§تا£»
£¨2£©دآءذثؤ¸ِ؛¯تح¼دَضذ؛¯تy=x+ ![]() µؤح¼دَ´َضآتا£»
µؤح¼دَ´َضآتا£» 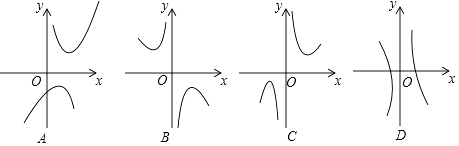
£¨3£©¶شسع؛¯تy=x+ ![]() £¬اَµ±x£¾0ت±£¬yµؤب،ضµ·¶خ§£® ا뽫دآءذµؤاَ½â¹³ج²¹³نحêصû£®
£¬اَµ±x£¾0ت±£¬yµؤب،ضµ·¶خ§£® ا뽫دآءذµؤاَ½â¹³ج²¹³نحêصû£®
½â£؛،كx£¾0
،ày=x+ ![]() =£¨
=£¨ ![]() £©2+£¨
£©2+£¨ ![]() £©2=£¨
£©2=£¨ ![]() ©پ
©پ ![]() £©2+
£©2+
،ك£¨ ![]() ©پ
©پ ![]() £©2،ف0
£©2،ف0
،ày،ف £®
£¨4£©بô؛¯تy= ![]() £¬شٍyµؤب،ضµ·¶خ§ £®
£¬شٍyµؤب،ضµ·¶خ§ £®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬OD تا،دAOB µؤئ½·ضدك£¬،دAOC=2،دBOC£®
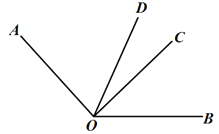
£¨1£©بô AO،حCO£¬اَ،دBOD µؤ¶بت£»
£¨2£©بô،دCOD=21،م£¬اَ،دAOB µؤ¶بت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬AB،خEF£¬شٍ،دA،¢،دC،¢،دD،¢،دEآْ×مµؤتء؟¹طدµتا£¨ £©

A. ،دA£«،دC£«،دD£«،دE£½360،م
B. ،دA£«،دD£½،دC£«،دE
C. ،دA£،دC£«،دD£«،دE£½180،م
D. ،دE£،دC£«،دD£،دA£½90،م
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com