
 动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4 (速度单位:单位长度/秒).
动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4 (速度单位:单位长度/秒).分析 (1)设动点A的速度是x单位长度/秒,那么动点B的速度是4x单位长度/秒,然后根据3秒后,两点相距15个单位长度即可列出方程解决问题;
(2)设x秒时,A、B两点到原点的距离恰好相等,那么A运动的长度为x,B运动的长度为4x,然后根据(1)的结果和已知条件即可列出方程解题.
解答 解:(1)设动点A的速度是x单位长度/秒,
根据题意得3(x+4x)=15
∴15x=15
解得:x=1,
则4x=4.
答:动点A的速度是1单位长度/秒,动点B的速度是4单位长度/秒;
标出A,B点如图,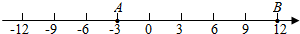 ;
;
(2)设x秒时,原点恰好处在两个动点的正中间,
根据题意得:3+x=12-4x
∴5x=9
∴x=$\frac{9}{5}$
答:$\frac{9}{5}$秒时,A、B两点到原点的距离恰好相等.
点评 本题考查了一元一次方程的应用和数轴.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
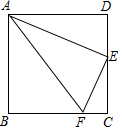 如图,边长为2的正方形ABCD中,E、F分别是BC、CD上的点(E、F与顶点不重合),∠AFD=90°.
如图,边长为2的正方形ABCD中,E、F分别是BC、CD上的点(E、F与顶点不重合),∠AFD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com