
【题目】已知如图,在数轴上点A,B所对应的数是-4,4.
![]()
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于-4,则称代数式N是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:
(1)关于x代数式|x-1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是____ ______.
所以代数式|x-1|__________(填是或不是)线段AB的封闭代数式.
(2)以下关x的代数式:
①![]() ;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
;②x2+1;③x2+|x|-8;④|x+2|-|x-1|-1.
是线段AB的封闭代数式是__________,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(![]() )关于x的代数式
)关于x的代数式![]() 是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
是线段AB的封闭代数式,则有理数a的最大值是__________,最小值是__________.
【答案】(1)5,0,不是;(2)④,理由见解析;(3)a的最大值是2,a的最小值是-14
【解析】
(1)根据绝对值的性质可求最值,再根据封闭代数式的定义即可求解;
(2)根据封闭代数式的定义即可求解;
(3)分两种情况讨论:![]() +3≤4,
+3≤4,![]() +3≥-4,依此即可求解.
+3≥-4,依此即可求解.
(1)解:当x=-4时,|x-1|取得最大值为5,
当x=1时,|x-1|取得最小值为0,
∵|x-1|的最大值>4,
∴|x-1|不是线段AB的封闭代数式.
(2)证明:①∵-4≤x≤4,
∴2≤![]() x≤2,
x≤2,
∴![]() ≤
≤![]() x
x![]() ≤
≤![]() ,
,
∵![]() x
x![]() 的最小值为
的最小值为![]() ,不满足最小值大于等于-4,
,不满足最小值大于等于-4,
∴![]() x
x![]() 不是线段AB的封闭代数式.
不是线段AB的封闭代数式.
②当x=±4时,
代数式x2+1取得最大值17,不满足最大值小于等于4,
∴x2+1不是线段AB的封闭代数式.
③当x=±4时,
代数式x2+|x|-8取得最大值12,不满足最大值小于等于4,
∴x2+|x|-8不是线段AB的封闭代数式.
④当-4≤x<-2时,
原式=|x+2|-|x-1|-1=-(x+2)+(x-1)-1=-4,
当-2≤x≤1时,
原式=|x+2|-|x-1|-1=(x+2)+(x-1)-1=2x,
∴-4≤2x≤2,
当1≤x≤4时,
原式=|x+2|-|x-1|-1=(x+2)-(x-1)-1=2,
综上所述:-4≤|x+2|-|x-1|-1≤2满足最大值小于等于4,最小值大于等于-4,
∴|x+2|-|x-1|-1是线段AB的封闭代数式.
(3)![]() +3≤4,
+3≤4,
a≤|x+1|+2,
|x+1|+2在-4和4之间的最小值是2,a要不大于这个最小值才能使所有在-4和4之间的x都成立,
所以a的最大值是2,
![]() +3≥-4,
+3≥-4,
a≥-7(|x+1|+2),
-7(|x+1|+2)在-4和4之间的最大值是-14,a要不小于这个最大值才能使所有在-4和4之间的x都成立,
所以a的最小值是-14.


科目:初中数学 来源: 题型:
【题目】一张长方形桌子可坐6人,按下图方式讲桌子拼在一起.
 ………
………
① ② ③
(1)观察图形,填写下表:
图形(n) | ② | ③ | …… | n |
坐的人数(人) | …… |
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改为每8张桌子拼成1张大桌子,则共可坐多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
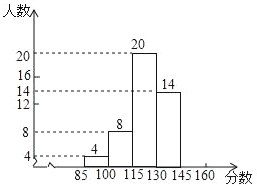
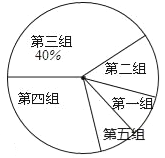
【题目】某公司为了掌握职工的工作成绩,随机抽取了部分职工的平时成绩(得分为整数,满分为160分)分为5组,第一组85~100;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
(1)写出本次调查共抽取的职工数为_____
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,求该公司1500名工作人员中,成绩评为“B”的人员大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
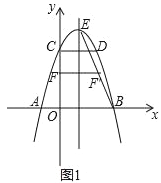
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC,点D在函数图象上,CD∥x轴且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图1,连BE,线段OC上的点F关于直线l的对称点F’恰好在线段BE上,求点F的坐标;
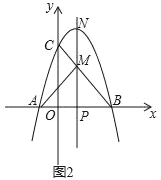
(3)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨和粗加工蔬菜16吨(两种加工不能同时进行)。
(1)如果要求在18天内全部销售这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,来不及精加工的进行粗加工,要求15天内刚好加工完这140吨蔬菜,则应如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
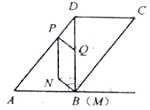
【题目】如图,BD是□ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD—DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),□PQMN与□ABCD重叠部分图形的面积为S(cm2).
(1)AP=_______cm(同含t的代数式表示).
(2)当点N落在边AB上时,求t的值.
(3)求S与t之间的函数关系式.
(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )

A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
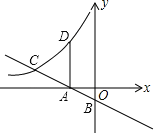
【题目】如图,直线y=-![]() x-
x-![]() 与x,y两轴分别交于A,B两点,与反比例函数y=
与x,y两轴分别交于A,B两点,与反比例函数y=![]() 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=![]() (x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.
(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com