
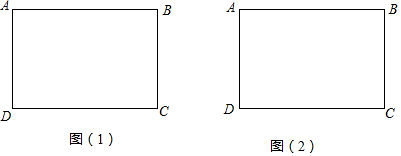
分析 (1)以线段AC的垂直平分线为对称轴,翻折即可.
(2)由△AFO≌△CEO,推出OE=FO,由∠ECO=∠ACD,∠EOC=∠D=90°,由△EOC∽△ADC,可得$\frac{OE}{AD}$=$\frac{OC}{DC}$,由此即可求出OE解决问题.
(3)将矩形ABCD沿对角线BD对折即可.
(4)利用勾股定理求出AC即可解决问题.
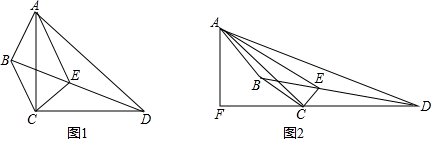
解答 解:(1)折叠后的图形如图1所示.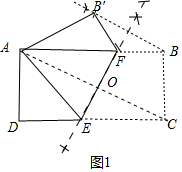
(2)∵四边形ABCD是矩形,
∴∠D=90°,AB=DC=8,AD=BC=6,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AB∥DC,
∴∠AFO=∠CEO,
∵OA=OC=5,∠AOF=∠EOC,
∴△AFO≌△CEO,
∴OE=FO,
∵∠ECO=∠ACD,∠EOC=∠D=90°,
∴△EOC∽△ADC,
∴$\frac{OE}{AD}$=$\frac{OC}{DC}$,
∴$\frac{OE}{6}$=$\frac{5}{8}$,
∴OE=$\frac{15}{4}$,
∴EF=2OE=$\frac{15}{2}$,
∴折痕EF的长为$\frac{15}{2}$.
(3)如图2中,折叠后的图形如图所示,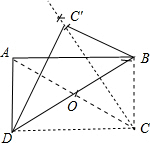
(4)∵四边形ABCD是矩形,
∴AC=BD,OC=OC,OB=OD,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$,
∴AO=$\frac{1}{2}$AC=$\frac{5\sqrt{5}}{2}$.
点评 本题考查四边形综合题、矩形的性质.相似三角形的判定和性质、勾股定理、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:选择题
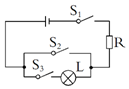 在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率( )
在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600(50-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
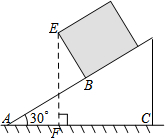 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m.
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com