
 如图,已知点P为正方形ABCD内一点,且PA=PB=5cm,点P到边CD的距离也为5cm,则正方形ABCD的面积为________cm2.
如图,已知点P为正方形ABCD内一点,且PA=PB=5cm,点P到边CD的距离也为5cm,则正方形ABCD的面积为________cm2. ,解直角△APF即可求得x的值.即可求得AB的长,根据AB的长即可求正方形ABCD的面积.
,解直角△APF即可求得x的值.即可求得AB的长,根据AB的长即可求正方形ABCD的面积. 解:过P作EF∥AD,则PE⊥CD,PF⊥AB,
解:过P作EF∥AD,则PE⊥CD,PF⊥AB, ,
, ,
,

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
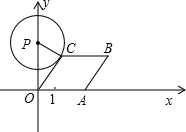 A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:
A为顶点作菱形OABC,使点B,C在第一象限内,且∠AOC=60°;以P(0,3)为圆心,PC为半径作圆.设点A运动了t秒,求:查看答案和解析>>
科目:初中数学 来源: 题型:
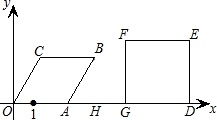 ,求出t的值;若不存在,请说明理由.
,求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
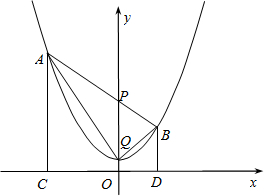 1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.
1个单位的速度向正方向运动,连接AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连接AQ、BQ.查看答案和解析>>
科目:初中数学 来源: 题型:
 x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂足为C、D,连结AQ、BQ.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省吴江市九年级5月教学调研测试数学试卷(解析版) 题型:解答题
如图,已知点A(−3,5)在抛物线y= x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以
x2+c的图象上,点P从抛物线的顶点Q出发,沿y轴以
每秒1个单位的速度向正方向运动,连结AP并延长,交抛物线于点B,分别过点A、B作x轴的垂线,垂
足为C、D,连结AQ、BQ.
(1)求抛物线的解析式;
(2)当A、Q、B三点构成以AQ为直角边的直角三角形时,求点P离开点Q多少时间?
(3)试探索当AP、AC、BP、BD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)时,点P离开点Q的时刻.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com