
 且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 3 |
| 2 |
| 25 |
| 8 |
(3-0)2+(
|
| 15 |
| 4 |
| 5 |
| 4 |
| 25 |
| 8 |
| 5 |
| 4 |
| 15 |
| 8 |
| 1 |
| 2 |
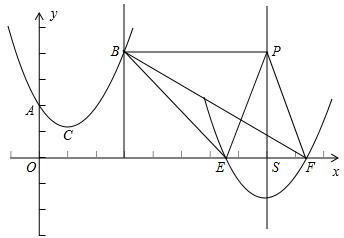 (3)二次函数平移后的解析式为y=
(3)二次函数平移后的解析式为y=| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
| ||
| 3 |
| 4t-5 |
| ||
| 3 |
| 4t-5 |
| ||
| 3 |
| 4t-5 |
2
| ||
| 3 |
| 4t-5 |
| 1 |
| 2 |
| ||
| 3 |
| 4t-5 |
| 17 |
| 4 |
| 1 |
| 3 |
| 413 |
| 64 |
| 413 |
| 64 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
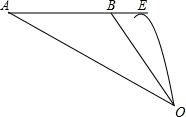 60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.
60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.查看答案和解析>>
科目:初中数学 来源: 题型:
| A | B | |
| 成本价(元/套) | 250 | 280 |
| 售价(元/套) | 300 | 340 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com