Question

【题目】在△ABC中，AB=2，AC=，∠B=30°.求∠BAC的度数.

Answer 1

【答案】∠BAC的度数为105°或15°.

【解析】试题分析:本题考查解直角三角形,由于题目没有给出△ABC的形状,所以要将∠BAC分为钝角和锐角进行分类分析,可过点A作AD⊥BC,在Rt△ADB中,结合已知的条件可求出∠BAD和AD, 在Rt△ADC中,结合已知条件AD和AC,利用锐角三角函数可求出∠CAD,再结合图形求出∠BAC.

解:(1)如图①，当∠BAC是钝角时，过点A作AD⊥BC，垂足为点D.在Rt△ABD中，∵∠B=30°，

∴∠BAD=60°，AD=AB·sin 30°=1.

在Rt△ACD中，CD===1，

∴△ACD是等腰直角三角形，则∠CAD=45°，

∴∠BAC=∠BAD+∠CAD=60°+45°=105°.

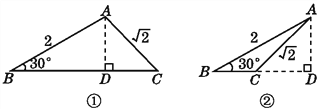
(2)如图②，当∠BAC是锐角时，过点A作AD⊥BC，交BC的延长线于点D.

∵∠B=30°，∴AD=AB·sin 30°=1，∠BAD=60°.

∴CD===1，

∴∠DAC=45°，

∴∠BAC=∠BAD-∠DAC=60°-45°=15°.

综上可知，∠BAC的度数为105°或15°.

常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角)，而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角)，从而造成漏解.