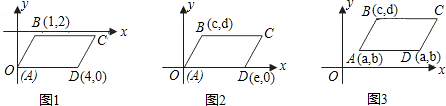
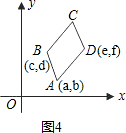
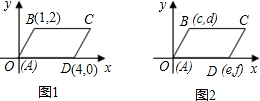解:(1)利用平行四边形的性质:对边平行且相等,
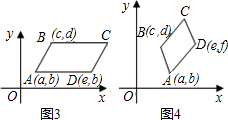
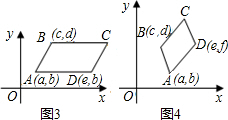
得出图1、图2,3中顶点C的坐标分别是:(5,2)、(e+c,d),(c+e-a,d).
故答案为:(5,2)、(e+c,d),(c+e-a,d).
(2)分别过点A,B,C,D作x轴的垂线,垂足分别为A
1,B
1,C
1,D
1,
分别过A,D作AE⊥BB
1于E,DF⊥CC
1于点F.
在平行四边形ABCD中,CD=BA,
又∵BB
1∥CC
1,
∴∠EBA+∠ABC+∠BCF=∠ABC+∠BCF+∠FCD=180度.
∴∠EBA=∠FCD.
又∵∠BEA=∠CFD=90°,
∴△BEA≌△CFD.
∴AE=DF=a-c,BE=CF=d-b.
设C(x,y).
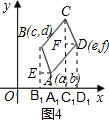
由e-x=a-c,得x=e+c-a.
由y-f=d-b,得y=f+d-b.
∴C(e+c-a,f+d-b).
(此问解法多种,可参照评分)
(3)m=c+e-a,n=d+f-b或m+a=c+e,n+b=d+f.
(4)若GS为平行四边形的对角线,由(3)可得P
1(-2c,7c).
要使P
1在双曲线上,
则有-14c
2=-14,
∴c
1=-1(根据其中c>0,舍去),c
2=1.此时P
1(-2,7).
若SH为平行四边形的对角线,由(3)可得P
2(3c,2c),
同理可得c=1,此时P
2(3,2)不在双曲线上.
若GH为平行四边形的对角线,由(3)可得(c,-2c),
同理可得c=1,此时P
3(1,-2)不在双曲线上.
综上所述,当c=1时,双曲线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形.
符合条件的点有P
1(-2,7).
分析:(1)根据平行四边形的性质:对边平行且相等,得出图2,3中顶点C的坐标分别是(e+c,d),(c+e-a,d);
(2)分别过点A,B,C,D作x轴的垂线,垂足分别为A
1,B
1,C
1,D
1,分别过A,D作AE⊥BB
1于E,DF⊥CC
1于点F.在平行四边形ABCD中,CD=BA,根据内角和定理,又∵BB
1∥CC
1,可推出∠EBA=∠FCD,△BEA≌△CFD.依题意得出AF=DF=a-c,BE=CF=d-b.设C(x,y).由e-x=a-c,得x=e+c-a.由y-f=d-b,得y=f+d-b.继而推出点C的坐标.
(3)在平行四边形ABCD中,CD=BA,同理证明△BEA≌△CFD(同(2)证明).然后推出AF=DF=a-c,BE=CF=d-b.又已知C点的坐标为(m,n),e-m=a-c,故m=e+c-a.由n-f=d-b,得出n=f+d-b.
(4)若GS为平行四边形的对角线,由(3)可得P
1(-2c,7c).要使P
1在双曲线上,则有-14c
2=-14,求出c的实际取值以及P
1的坐标,若SH为平行四边形的对角线,由(3)可得P
2(3c,2c),同理可得c=1,此时P
2(3,2);若GH为平行四边形的对角线,由(3)可得(c,-2c),同理可得c=1,此时P
3(1,-2);故综上所述可得解.
点评:此题主要考查了平行四边形的性质,平面直角坐标系内的坐标,平行线的性质等知识.理解平行四边形的特点结合平面直角坐标系是解决本题的关键.

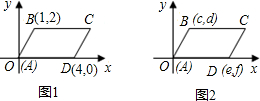
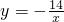 和三个点
和三个点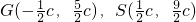 ,H(2c,0)(其中c>0).问当c为何值时,该双曲线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
,H(2c,0)(其中c>0).问当c为何值时,该双曲线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.


 请阅读下列材料:
请阅读下列材料: 如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.
如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.