
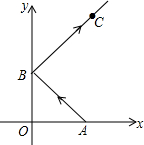
 如图,从点A(2,0)发出的一束光,经y轴反射,过点C(3,5),则B点的坐标为(0,2).
如图,从点A(2,0)发出的一束光,经y轴反射,过点C(3,5),则B点的坐标为(0,2). 分析 先作CD⊥y轴于D,由A(2,0),C(3,5),得OA=2,CD=3,OD=5,BD=5-OB,在证△AOB∽△BDC,根据相似三角形的对应边成比例,得$\frac{OA}{CD}=\frac{OB}{BD}$,即可得到结论.
解答 解:如图,过点C作CD⊥y轴于D,
∵A(2,0),C(3,5),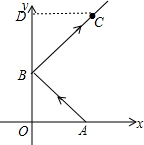
∴OA=2,CD=3,OD=5,
∴BD=5-OB,
根据题意得:∠ABO=∠CBD,
∵∠AOB=∠BDC=90°,
∴△AOB∽△BDC,
∴$\frac{OA}{CD}=\frac{OB}{BD}$,
即$\frac{2}{3}=\frac{OB}{5-OB}$,
解得:OB=2,
B点的坐标为(0,2)
故答案为(0,2).
点评 此题考查了相似三角形的判定与性质以及点与坐标的性质.此题难度适中,解此题的关键是掌握辅助线的作法,掌握入射光线与反射光线的关系.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?
如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
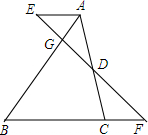 如图,在△ABC中,D是AC的中点,AE∥BC,DE交AB于点G,交BC的延长线于点F,若BG:AG=3:1,BC=10,则线段AE的长为( )
如图,在△ABC中,D是AC的中点,AE∥BC,DE交AB于点G,交BC的延长线于点F,若BG:AG=3:1,BC=10,则线段AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
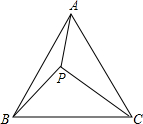 数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断
数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com