
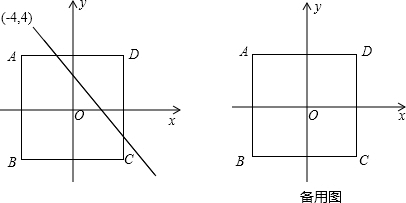
分析 (1)线段AB与CD的“密距”是AD或BC的长度;
(2)先求得直线OA的解析式,可知直线EF与OA垂直,故点C到直线EF的距离为“疏距”;
(3)当O、K、D在一条直线上时,密距有最小值,当OK⊥AD时,密距有最大值.
解答  解:(1)如图1所示:
解:(1)如图1所示:
由垂线的性质可知:线段AB与CD的“密距”是AD或BC的长度,
故“密距”是8.
在Rt△ADC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=8$\sqrt{2}$,
“疏距”是8$\sqrt{2}$;
故答案为:8;8$\sqrt{2}$;
(2)如图2所示:
设直线OD的解析式为y=kx,
将x=4,y=4代入函数的解析式得4=4k,
解得:k=1,
∵直线EF的解析式为y=-$\frac{3}{4}$x+b,
∴直线OB和EF相互垂直.
∵EF与矩形ABCD的“密距”是1,
∴点D到EF的距离最长=8$\sqrt{2}$+1,
即“疏距”=8$\sqrt{2}$+1;
(3)①当K在BD上时,
如图3所示: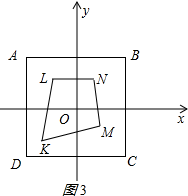 正方形ABCD与四边形KLMN的“疏距”为KB=4$\sqrt{2}$+2,
正方形ABCD与四边形KLMN的“疏距”为KB=4$\sqrt{2}$+2,
∴KD=BD-BK=8$\sqrt{2}$-(4$\sqrt{2}$+2)=4$\sqrt{2}$-2,
故最大密距=4$\sqrt{2}$-2;
②当OK⊥AD时,
如图4所示:
正方形ABCD与四边形KLMN的“密距”有最小值,
∵正方形的边长为8,
∴O到AD的距离为4, 又由①可知OK=OD-KD=4$\sqrt{2}$-(4$\sqrt{2}$-2)=2,
又由①可知OK=OD-KD=4$\sqrt{2}$-(4$\sqrt{2}$-2)=2,
所以密距的最小值=4-OK=4-2=2,
故密距的范围为:2≤密距≤4$\sqrt{2}$-2.
点评 本题是一次函数综合题目,考查了一次函数解析式的求法、勾股定理、两点间的距离、点到直线的距离等知识;本题综合性强,根据题意画出图形是解决问题的关键.题目较为新颖,难度适中.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.
如图,在⊙O中,弦EF∥直径AB,如果$\widehat{AE}$的度数为50°,那么$\widehat{BF}$的度数为50°,∠BOF=50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
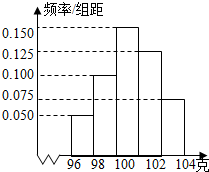 如图是抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
如图是抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A. | 90 | B. | 108 | C. | 60 | D. | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com