
 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.分析 (1)根据图象可以设从甲地到乙地时的函数关系式为:y=kx,代入点(1.5,60),即可得解,再设从乙地回到甲地的函数关系式为:y=mx+n(m、n是常数,m≠0),代入点(2,60),(3,0),即可得解;
(2)将x=2.5代入即可.
解答 解:(1)设从甲地到乙地时的函数关系式为:y=kx,(k是常数,k≠0)则:
1.5k=60,
解得:k=40,
∴y=40x(0≤x≤1.5);
设从乙地回到甲地的函数关系式为:y=mx+n(m、n是常数,m≠0),则:
$\left\{\begin{array}{l}{2m+n=60}\\{3m+n=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-60}\\{n=180}\end{array}\right.$.
∴y=-60x+180(2≤x≤3);
(2)当x=2.5时,y=-60×2.5+180=30(km),
即汽车出发后2.5小时,汽车距甲地30km.
点评 本题主要考查了根据图象写出一次函数的解析式,解题的关键是在图象中找出点的坐标,还考查了函数值的问题,是经常考查的题目,注意总结.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
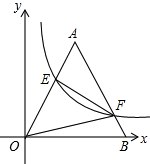 若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.
若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2是不等式3x>5的一个解 | B. | x=2是不等式3x>5的解 | ||
| C. | x=2是不等式3x>5的唯一解 | D. | x=2不是不等式3x>5的解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com