
【题目】(1)验证下列两组数值的关系:
2sin30°cos30°与sin60°;
2sin22.5°cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
【答案】(1)![]() ;
;![]() ;0.7;0.7;(2)一个角正弦与余弦积的2倍,等于该角2倍的正弦值;(3)结论成立;(4)2sinαcosα=sin2α.
;0.7;0.7;(2)一个角正弦与余弦积的2倍,等于该角2倍的正弦值;(3)结论成立;(4)2sinαcosα=sin2α.
【解析】
(1)分别计算出各数,进而可得出结论;
(2)根据(1)中的关系可得出结论;
(3)任选一个角验证(3)的结论即可;
(4)用α表示一个锐角,写出这个关系式即可.
(1)∵2sin30°cos30°=2![]() ,sin60°
,sin60°![]() .
.
2sin22.5°cos22.5≈2×0.38×0.92≈0.7,sin45°![]() 0.7,∴2sin30°cos30°=sin60°,2sin22.5°cos22.5=sin45°;
0.7,∴2sin30°cos30°=sin60°,2sin22.5°cos22.5=sin45°;
(2)由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)2sin15°cos15°≈2×0.26×0.97![]() ,sin30°
,sin30°![]() ;
;
故结论成立;
(4)2sinαcosα=sin2α.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
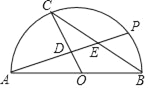
【题目】P是以AB为直径的半圆上一动点(P与A、B不重合),O为圆心,CO⊥AP,OC、BC与AP分别相交于D、E两点,AB=12.
(1)若∠ABC=35°,求∠PAB的度数;
(2)若AP平分线段BC,求弦AP的长度;
(3)是否存在点P,使△PBC的面积为整数,如果存在,这样的P点有几个?(直接写出结果,不需写出解题过程.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平底面A处安置侧倾器测得楼房CD顶部点D的仰角为30°,向前走20米到达E处,测得点D的仰角为60°.已知侧倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米)( )
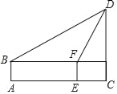
A. 30米 B. 18.9米 C. 32.6米 D. 30.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
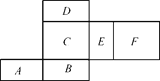
【题目】如图是一个多面体的展开图,每个面上都标注了字母,请你根据要求回答问题:
(1)这个多面体是一个什么物体?
(2)如果D是多面体的底部,那么哪一面会在上面?
(3)如果B在前面,C在左面,那么哪一面在上面?
(4)如果E在右面,F在后面,那么哪一面会在上面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,22,3分)如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.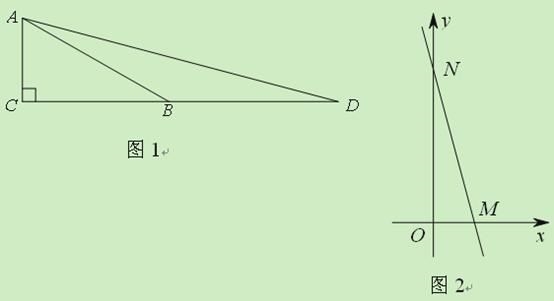
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
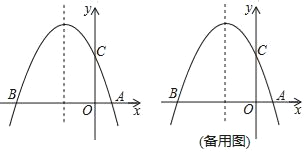
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com