解:AE=DC,但BF≠BG.
理由(1)AE=DC.
∵△ABD和等边△BCE,
∴AB=BD,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠DBE=∠CBE+∠DBE,
即∠ABE=∠CBD,
∴△ABE≌△DBC(SAS).
∴AE=DC(全等三角形对应边相等),
∠BAE=∠BDC(全等三角形对应角相等).
(2)BF≠BG.
理由:若BG=BF,由(1)可知△ABE≌△DBC,
∴∠BAF=∠BDG,
又AB=DB
则△ABF与△DBG有两边和一边的对角对应相等.
∴∠ABF=∠DBG或∠ABG+∠DBG=180°(不合题意,舍去)
∴△ABF≌△DBG(SAS).
∴∠ABF=∠DBG=60°(全等三角形对应角相等).
∴∠ABF=∠DBG=60°=∠CBE,
所以A、B、C在同一条直线上,这与题意A、B、C不在同一直线上矛盾,
∴BF≠BG.
另法:BF≠BG
上面已证明∠BCD=∠BEA
假如BF=BG(边),又BC=BE(等边三角形之边)
则必须∠EBF=60°(两边夹角)
才能使△BCG≌△BEF(SAS)
而现在的∠EBF是任意的.“A,B,C三点不在一条直线上”.
如果“A,B,C三点不在一条直线上”,且∠ABC=120°,
则BF=BG.
分析:要说明AE=DC和BF=BG是否成立,因为它们在不同的三角形中,所以可证两个三角形全等,分别说明是否成立.由题意知等边△ABD和等边△BCE得:AB=BD,BC=BE,∠ABD=∠CBE=60°,所以可得△ABE≌△DBC可说明AE=DC.而BF=BG是否成立,可在△ABF和△DBG中加以说明,若BF=BG,则可证△ABF≌△DBG,全等三角形的对应角相等,则有∠ABF=∠DBG=60°=∠CBE,这个式子说明A、B、C三点同线,与题意不符,所以二者不相等.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;证明线段不相等是比较独特的,要注意掌握.

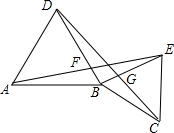 附加题:如图,如果A、B、C不在一条直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G,那么AE=DC和BF=BG成立?并请加以说明.
附加题:如图,如果A、B、C不在一条直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G,那么AE=DC和BF=BG成立?并请加以说明.


 36、附加题:如图,如果A、B、C不在一条直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G,那么AE=DC和BF=BG成立?并请加以说明.
36、附加题:如图,如果A、B、C不在一条直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G,那么AE=DC和BF=BG成立?并请加以说明.