
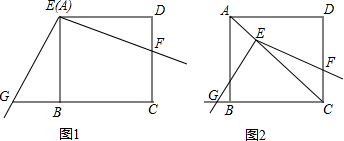
分析 (1)由∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,可得∠DEF=∠GEB,又由正方形的性质,可利用ASA证得Rt△FED≌Rt△GEB,则问题得证;
(2)①首先过点E分别作BC、CD的垂线,垂足分别为H、P,然后利用ASA证得Rt△FEP≌Rt△GEH,则问题得证;
②借助①的结论得出S△FEP=S△GEH,进而S四边形EFCG=S四边形EPCG=$\frac{1}{2}$EH2=2即可.
解答 (1)证明:∵∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,
∴∠DEF=∠GEB,
在△FED和△GEB中,$\left\{\begin{array}{l}{∠DEF=∠GEB}\\{ED=EB}\\{∠D=∠EBG}\end{array}\right.$,
∴△FED≌△GEB(ASA),
∴EF=EG;
(2)①解:成立.
证明:如图2,过点E作EH⊥BC于H,过点E作EP⊥CD于P,
∵四边形ABCD为正方形,
∴CE平分∠BCD,
又∵EH⊥BC,EP⊥CD,
∴EH=EP,
∴四边形EHCP是正方形,
∴∠HEP=90°,
∵∠GEH+∠HEF=90°,∠PEF+∠HEF=90°,
∴∠PEF=∠GEH,
∴在Rt△FEP与Rt△GEH中,$\left\{\begin{array}{l}{∠PEF=∠GEH}\\{∠EPF=∠EHG}\\{EP=EH}\end{array}\right.$,
∴△FEP≌△GEH(AAS),
∴EF=EG;
②由①知,四边形EHCP是正方形,
∵EC=2,
∴EH=$\sqrt{2}$
由①知,△FEP≌△GEH,
∴S△FEP=S△GEH,
∴S四边形EFCG=S四边形EPCG=$\frac{1}{2}$EH2=2
点评 此题是四边形综合题,主要考查了正方形的性质,全等三角形的判定和性质,解(1)的关键是判断出△FED≌△GEB,解(2)的关键是判断出∠PEF=∠GEH,是一道中等难度的中考常考题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
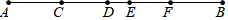 如图,C、D、E、F为线段AB上顺次排列的4个动点(不与A、B重合),图中共有15条线段.若AB=8.6cm,DE=1cm,图中所有线段长度之和为56cm,则线段CF长为4cm.
如图,C、D、E、F为线段AB上顺次排列的4个动点(不与A、B重合),图中共有15条线段.若AB=8.6cm,DE=1cm,图中所有线段长度之和为56cm,则线段CF长为4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
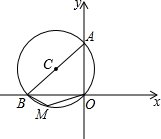 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,4),M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径长为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,4),M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径长为( )| A. | 5 | B. | 4 | C. | 3 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.
如图,?ABCD中,∠B=45°,AC⊥BC,E是CA延长线上一点,O是AB的中点,连接OE,交DA延长线与点H,过点O作OG⊥OE交AC于点F,交BC的延长线于点G,连接CO.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com