
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
【答案】(1)3;(2)![]() ;(3)n>0
;(3)n>0
【解析】
(1)观察已知表格中的对应值可知:该函数图象的开口向上,对称轴是直线x=1,由抛物线的对称性可知:x=3时的对应函数值与x= -1时的对应函数值相等,即可求得![]() 的值;
的值;
(2)把表中的三个点![]() 、(1,-1)、(2, 0)代入函数的解析式,得到关于a,b,c的方程组,即可求得解析式;
、(1,-1)、(2, 0)代入函数的解析式,得到关于a,b,c的方程组,即可求得解析式;
(3)根据函数的图象开口方向,增减性即可确定.
(1)观察已知表格中的对应值可知:该函数图象的开口向上,对称轴是直线x=1,
∴由抛物线的对称性可知:x=3时的对应函数值与x= -1时的对应函数值相等,即m的值为3;
(2)把![]() 、(1,-1)、(2, 0)代入二次函数
、(1,-1)、(2, 0)代入二次函数![]()
![]() ,得
,得
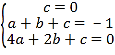 ,
,
解得: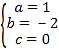
∴这个二次函数的解析式为![]() ;
;
(3)∵该函数图象的开口向上,对称轴是直线x=1,
∴若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,则
点A(n+2,y1),B(n,y2)在对称轴两侧时,n+2-1![]() 1-n且
1-n且![]() ,
,
解得:![]() ;
;
点A(n+2,y1),B(n,y2)在对称轴同侧(含顶点)时,![]() ,
,
综上可知:n的取值范围是n![]() .
.


科目:初中数学 来源: 题型:
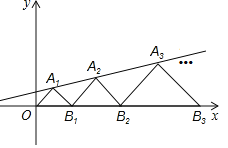
【题目】如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
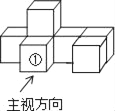
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某绿色种植基地种植的农产品喜获丰收,此基地将该农产品以每千克5元出售,这样每天可售出1500千克,但由于同类农产品的大量上市,该基地准备降价促销,经调查发现,在本地该农产品若每降价![]() 元,每天可多售出100千克
元,每天可多售出100千克![]() 当本地销售单价为
当本地销售单价为![]() 元时,销售量为y千克.
元时,销售量为y千克.
![]() 请直接写出y和x的函数关系式;
请直接写出y和x的函数关系式;
![]() 求在本地当销售单价为多少时可以获得最大销售收入?最大销售收入是多少?
求在本地当销售单价为多少时可以获得最大销售收入?最大销售收入是多少?
![]() 若该农产品不能在一周内出售,将会因变质而不能出售
若该农产品不能在一周内出售,将会因变质而不能出售![]() 依此情况,基地将10000千克该农产品运往外地销售
依此情况,基地将10000千克该农产品运往外地销售![]() 已知这10000千克农产品运到了外地,并在当天全部售完
已知这10000千克农产品运到了外地,并在当天全部售完![]() 外地销售这种农产品的价格比在本地取得最大销售收入时的单价还高
外地销售这种农产品的价格比在本地取得最大销售收入时的单价还高![]() ,而在运输过程中有
,而在运输过程中有![]() 损耗,这样这一天的销售收入为42000元
损耗,这样这一天的销售收入为42000元![]() 请计算出a的值.
请计算出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
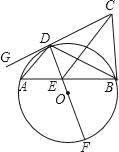
【题目】如图,⊙O的直径DF与弦AB交于点E,C为⊙O外一点,CB⊥AB,G是直线CD上一点,∠ADG=∠ABD.
求证:ADCE=DEDF;
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路过程写出来(要求至少写3步);
(2)在你经历说明(1)的过程之后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
①∠CDB=∠CEB;
②AD∥EC;
③∠DEC=∠ADF,且∠CDE=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
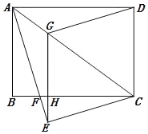
【题目】如图,把矩形ABCD沿AC折叠,使点D与点E重合,AE交BC于点F,过点E作EG∥CD交AC于点G,交CF于点H,连接DG.
(1)求证:四边形ECDG是菱形;
(2)若DG=6,AG=![]() ,求EH的值.
,求EH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
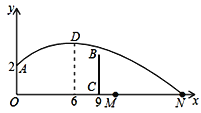
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个不透明的口袋中装有5个只有颜色不同的球,其中2个白球,3个黑球![]() 第一次随机摸出一个球,不放回,再随机摸出一个球.
第一次随机摸出一个球,不放回,再随机摸出一个球.
![]() Ⅰ
Ⅰ![]() 求第一次摸到黑球的概率;
求第一次摸到黑球的概率;
![]() Ⅱ
Ⅱ![]() 请用列表或画树状图等方法求两次都摸到黑球的概率.
请用列表或画树状图等方法求两次都摸到黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
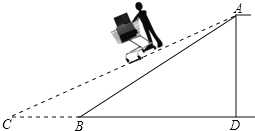
【题目】某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1:1.8改为1:2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com