
如下图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
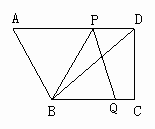
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.
|
(1)如下图,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形.
∴PM=DC=12∵QB=16-t, ∴S= (2)由图可知:CM=PD=2t,CQ=t.以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况: ①若PQ=BQ.在Rt△PMQ中, 由PQ2=BQ2得 ②若BP=BQ.在Rt△PMB中, 由于Δ=-704<0 ∴ ③若PB=PQ.由PB2=PQ2,得 整理,得 综合上面的讨论可知:当t= (3)如下图,由△OAP∽△OBQ,得
∵AP=2t-21,BQ=16-t,∴2(2t-21)=16-t. ∴t= 过点Q作QE⊥AD,垂足为E, ∵PD=2t,ED=QC=t,∴PE=t. 在RT△PEQ中,tan∠QPE= (4)设存在时刻t,使得PQ⊥BD.如下图,
过点Q作QE⊥ADS,垂足为E. 由Rt△BDC∽Rt△QPE,得 所以,当t=9秒时,PQ⊥BD. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
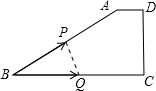 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=6cm,AD=2cm,动点P、Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P点运动的时间为t(s),△BPQ的面积为y(cm2).下图中能正确表示整个运动中y关于t的函数关系的大致图象是( )
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,CD=6cm,AD=2cm,动点P、Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到C点停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P点运动的时间为t(s),△BPQ的面积为y(cm2).下图中能正确表示整个运动中y关于t的函数关系的大致图象是( )A、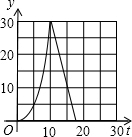 | B、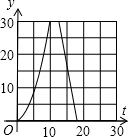 | C、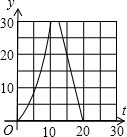 | D、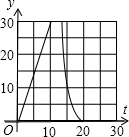 |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:013
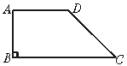
A.8,4![]() B.8
cm,(4.5+4
B.8
cm,(4.5+4![]() ) cm
) cm
C.4(![]() +1)+
+1)+![]() ,8 D.8
cm,(4
,8 D.8
cm,(4![]() +4) cm
+4) cm
查看答案和解析>>
科目:初中数学 来源:2009年重庆市中考数学试卷 题型:044
已知:如下图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.

(1)求证:BG=FG;
(2)若AD=DC=2,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com