
如图1,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.

(1)在Rt△ABC中, AB=6,AC=8,所以BC=10. 在Rt△CDE中,CD=5
,所以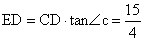
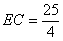 .(2分)
.(2分)
(2)如图2,过点D作DM⊥AB,DN⊥AC,垂足分别为M、N,那么DM、DN是△ABC的两条中位线,DM=4,DN=3. 由∠PDQ=90°,∠MDN=90°,可得∠PDM=∠QDN.
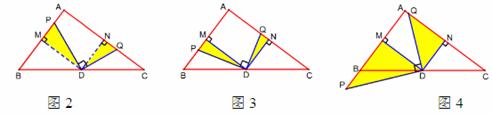 因此△PDM∽△QDN.所以
因此△PDM∽△QDN.所以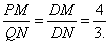
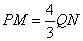
①如图3,当BP=2,P在BM上时,PM=1.
此时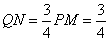 所以
所以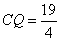
②如图4,当BP=2,P在MB的延长线上时,PM=5.
此时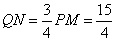
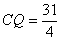 (4分)
(4分)
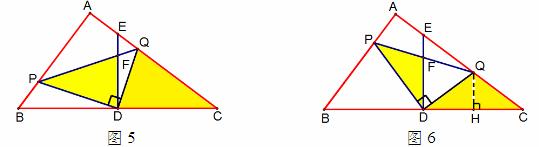
(3)如图5,如图2,在Rt△PDQ中,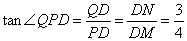 .
.
在Rt△ABC中,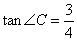 .所以∠QPD=∠C. 由∠PDQ=90°,∠CDE=90°,可得∠PDF=∠CDQ. 因此△PDF∽△CDQ. 当△PDF是等腰三角形时,△CDQ也是等腰三角形. ①如图5,当CQ=CD=5时,QN=CQ-CN=5-4=1(如图3所示).
.所以∠QPD=∠C. 由∠PDQ=90°,∠CDE=90°,可得∠PDF=∠CDQ. 因此△PDF∽△CDQ. 当△PDF是等腰三角形时,△CDQ也是等腰三角形. ①如图5,当CQ=CD=5时,QN=CQ-CN=5-4=1(如图3所示).
此时
.所以BP=BM-PM=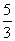 . ②如图6,当QC=QD
. ②如图6,当QC=QD
时,由cosC=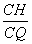 ,
,
所以QN=CN-CQ=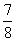 (如图2所示) .
(如图2所示) .
此时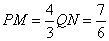 .所以
.所以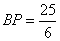 . ③不存在DP=DF的情况.这是因为∠DFP≥∠DQP>∠DPQ(如图5,图6所示).(6分)
. ③不存在DP=DF的情况.这是因为∠DFP≥∠DQP>∠DPQ(如图5,图6所示).(6分)


科目:初中数学 来源: 题型:
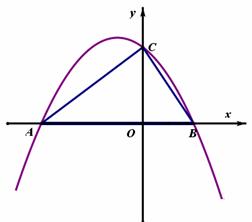
如图,抛物线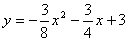 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上一动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
为了增强体质并迎接即将到来的体育中考,全校学生积极参加体育锻炼,学校教务处对学生锻炼时间做了一抽样调查,记录了部分学生锻炼时间如下:
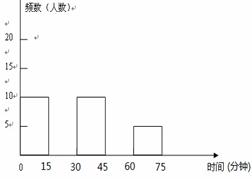
| 时间分组(分钟) | 频数(人数) | 频率 |
| 0≤t<15 | 10 | 0.2 |
| 15≤t<30 | 0.4 | |
| 30≤t<45 | 10 | 0.2 |
| 45≤t<60 | 0.1 | |
| 60≤t<75 | 5 | |
| 合计 | 1 |
(1)请你将频数分布表和频数分布直方图补充完整。
(2)上述学生的锻炼时间的中位数落在哪一组范围内?
(3)请估计全校350名九年级学生中约有多少学生时间在45分钟以内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com