
分析 (1)设甲每天加工x个A型零件,则乙每天加工(35-x)个B型零件,根据题意,易得$\frac{60}{x}$=$\frac{80}{35-x}$,解方程可得x的值,进而可得答案;
(2)根据题意,可得关系式P=15m+20(m-1),化简可得P=35m-20,根据一次函数的性质分析可得答案.
解答 解:(1)设甲每天加工x个A型零件,则乙每天加工(35-x)个B型零件,根据题意,
易得$\frac{60}{x}$=$\frac{80}{35-x}$,
解得x=15,
经检验,x=15是原方程的解,且符合题意.
35-15=20(个).
答:甲每天加工15个A型零件,则乙每天加工20个B型零件;
(2)P=15m+20(m-1),
即P=35m-20,
∵在P=35m-20中,P是m的一次函数,k=35>0,P随m的增大而增大,
又由已知得:3≤m≤5,
∴当m=5时,P的最大值=155,
当m=3时,P的最小值=85.
点评 此题主要考查了分式方程的应用,能根据题意,列出关系式,进而结合一次函数的性质得到结论或求解方程是解题关键.


科目:初中数学 来源: 题型:填空题
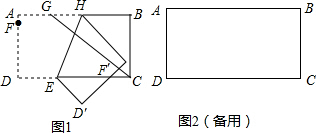
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
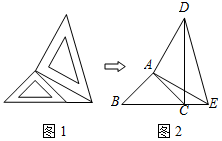 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
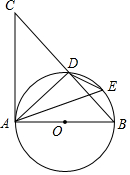 如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是$\widehat{BD}$上一点.
如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是$\widehat{BD}$上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com