
【题目】在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角,其顶点都在格点上,若点A、C的坐标分别为(﹣5,﹣2)和(﹣1,0). 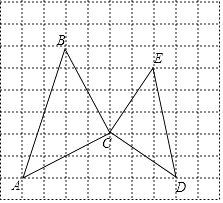
(1)建立平面直角坐标系,写出点B、D、E的坐标;
(2)求△ABC的面积.
科目:初中数学 来源: 题型:
【题目】为寻求合适的销售价格,商场对新进的一种商品进行了一周的试销,发现这种商品的每天销售量y(千克)与销售价格x(元/千克)之间成反比例关系.已知第一天以220元/千克的价格销售了80千克.
(1)求y与x的函数关系式.
(2)试销期间共销售了700千克这种新进商品,在试销后,商场决定将这种新进商品的销售价格定为160元/千克,这样按所发现的反比例关系预测剩余这种商品再用10天可以全部售完.问商场共新进多少千克的这种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H. 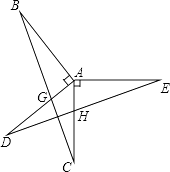
求证:
(1)△ABC≌△ADE;
(2)BC⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】马师傅计划用10天时间完成加工320个零件,前二天每天加工20个零件,后改进了工作方式,结果提前一天并超额完成了加工任务,若设马师傅在二天后每天至少加工x个零件,请你列出x所满足的不等式并求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识背景】在学习计算框图时,可以用“ ![]() ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ![]() ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ![]() ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) 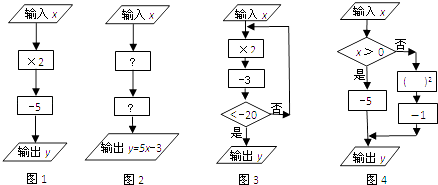
【尝试解决】
(1)①如图1,当输入数x=﹣2时,输出数y=;
②如图2,第一个“ ![]() ”内,应填; 第二个“
”内,应填; 第二个“ ![]() ”内,应填;
”内,应填;
(2)①如图3,当输入数x=﹣1时,输出数y=;②如图4,当输出的值y=17,则输入的值x=;
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量x,输出数为水费y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(3,y1),B(5,y2),C(﹣2,y3)是抛物线y=﹣x2+4x+k上的三点,则y1、y2、y3的大小关系为( )
A.y2>y1>y3
B.y3>y2>y1
C.y1>y2>y3
D.y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点. ![]()
(1)若AB=10cm,则MN=cm;
(2)若AC=3cm,CP=1cm,求线段PN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com