
【题目】A,B两地之间有一条6000米长的直线跑道,小月和小华分别从A,B两地同时出发匀速跑步,相向而行,第一次相遇后,小月将自己的速度提高25%,并匀速跑步到达B点,到达后原地休息;小华匀速跑步到达A点后,立即调头按原速返回B点(调头时间忽略不计),两人距各自出发点的距离之和记为y(米),跑步时间记为x(分钟),已知y(米)与x(分钟)之间的关系如图所示,则小月到达B点后,再经过_____分钟小华回到B点.

科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C(![]() ,0)作CD交AB于D,交
,0)作CD交AB于D,交![]() 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.

(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勤俭节约一直是中华民族的传统美德,某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛,为此先对同学们每月零花钱的数额进行一些了解,随机调查了本校部分同学,根据调查结果绘制出了如下两个尚不完整的统计图表.
组别 | 分组(单位:元) | 人数 |
|
| 4 |
|
|
|
|
|
|
|
| 8 |
|
| 2 |
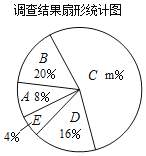
根据统计图表中的信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)扇形统计图中扇形![]() 的圆心角的度数为
的圆心角的度数为 ![]() ;所抽取同学零花钱的数额的中位数落在 范围;
;所抽取同学零花钱的数额的中位数落在 范围;
(3)该校共有1200名学生,请估计每月零花钱的数额在![]() 范围的人数.
范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.
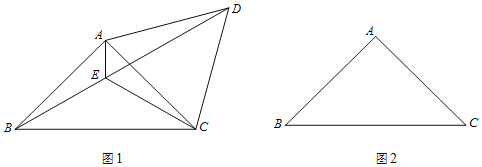
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,
(1)请问工厂平均每月降低率为多少?
(2)该工厂将产品投放市场进行实销,经过调查,得到如下数据:
销售单价 | …… | 40 | 50 | 60 | 70 | …… |
每天销售量 | …… | 400 | 300 | 200 | 100 | …… |
把上表中![]() 、
、![]() 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想![]() 与
与![]() 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
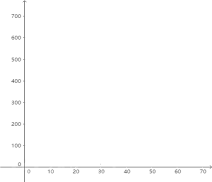
(3)当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠BAD=∠BDC=90°,AB=AD,∠DCB=60°,CD=8.
(1)若P是BD上一点,且PA=CD,求∠PAB的度数.
(2)①将图1中的△ABD绕点B顺时针旋转30°,点D落在边BC上的E处,AE交BD于点O,连接DE,如图2,求证:DE2=DODB;
②将图1中△ABD绕点B旋转α得到△A'BD'(A与A',D与D'是对应点),若CD'=CD,则cosα的值为 .

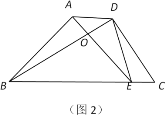
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:![]() 、
、![]() 都是关于
都是关于![]() 的多项式,
的多项式,![]() ,
,![]() ,其中多项式
,其中多项式![]() 有一项被“□”遮挡住了.
有一项被“□”遮挡住了.
(1)当![]() 时,
时,![]() ,请求出多项式
,请求出多项式![]() 被“□”遮挡的这一项的系数;
被“□”遮挡的这一项的系数;
(2)若![]() 是单项式,请直接写出多项式
是单项式,请直接写出多项式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com