Question

将Rt△ABC的直角顶点C与直角坐标系的原点O重合，两直角边与两坐标轴重合放在第一象限内，如果OA=3，OB=4．
（1）求斜边AB所在直线的函数解析式；
（2）若将△ABC绕C点旋转90°，求斜边AB旋转后所在直线的解析式．

Answer 1

分析：（1）Rt△ABC的放置方法有两种，分类考虑OA和OB分别与x轴重合的情况，无论哪一种情形，都可以先分别求出A、B两点的坐标，再运用待定系数法求解；
（2）图形绕某点旋转的确定条件是：方向和角度，此问题中隐含了方向，由（1）中求出的直线AB的解析式分顺时针旋转和逆时针旋转两种情况考虑．

解答：解：（1）设斜边AB所在直线的函数解析式为y=kx+b．
分两种情况：①当OA与x轴重合时，如图1．
∵OA=3，OB=4，点A、点B分别在x轴正半轴、y轴正半轴上，
∴A（3，0），B（0，4）．
将A（3，0），B（0，4）代入y=kx+b，
得

3k+b=0 b=4

，解得

k=- 4 3 b=4

．
∴斜边AB所在直线的函数解析式为l₁：y=-

4

3

x+4；
②当OB与x轴重合时，如图2．
∵OA=3，OB=4，点B、点A分别在x轴正半轴、y轴正半轴上，
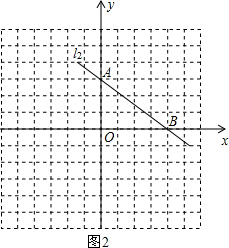
∴B（4，0），A（0，3）．
将B（4，0），A（0，3）代入y=kx+b，
得

4k+b=0 b=3

，解得

k=- 3 4 b=3

．
∴斜边AB所在直线的函数解析式为l₂：y=-

3

4

x+3．
综上可知，斜边AB所在直线的函数解析式为l₁：y=-

4

3

x+4或l₂：y₂=-

3

4

x+3；

（2）将△ABC绕C点（即原点）旋转90°时，直线AB也是绕C点（即原点）旋转90°，设斜边AB旋转后所在直线的解析式为y=mx+n．
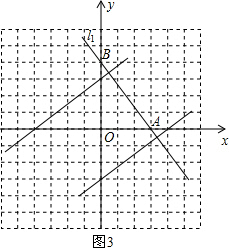
①对于直线l₁：y=-

4

3

x+4，如图3．
如果绕原点顺时针旋转90°，则A、B的对应点分别为（0，-3），（4，0），
将（0，-3），（4，0）代入y=mx+n，
得

n=-3 4m+n=0

，解得

m= 3 4 n=-3

．
即直线l₁：y=-

4

3

x+4绕原点顺时针旋转90°后所在直线的解析式为y=

3

4

x-3；
如果绕原点逆时针旋转90°，则A、B的对应点分别为（0，3），（-4，0），
将（0，3），（-4，0）代入y=mx+n，
得

n=3 -4m+n=0

，解得

m= 3 4 n=3

．
即直线l₁：y=-

4

3

x+4绕原点逆时针旋转90°后所在直线的解析式为y=

3

4

x+3；
②对于直线l₂：y=-

3

4

x+3，如图4．
如果绕原点顺时针旋转90°，则A、B的对应点分别为（3，0），（0，-4），
将（3，0），（0，-4）代入y=mx+n，
得

3m+n=0 n=-4

，解得

m= 4 3 n=-4

．
即直线l₂：y=-

3

4

x+3绕原点顺时针旋转90°后所在直线的解析式为y=

4

3

x-4；
如果绕原点逆时针旋转90°，则A、B的对应点分别为（-3，0），（0，4），
将（-3，0），（0，4）代入y=mx+n，
得

-3m+n=0 n=4

，解得

m= 4 3 n=4

．
即直线l₂：y=-

3

4

x+3绕原点逆时针旋转90°后所在直线的解析式为y=

4

3

x+4；
综上可知，斜边AB旋转后所在直线的解析式为y=

3

4

x±3或y=

4

3

x±4．

点评：本题是一次函数的综合题，其中涉及到运用待定系数法求直线的解析式，旋转的定义及性质，进行分类讨论是解题的关键，本题难度虽然不大，但是容易漏掉情况．