
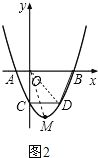
����Ŀ����ͼ1��������y=x2��2x+k��x�ύ��A��B���㣬��y�ύ�ڵ�C��0����3����[ͼ2��ͼ3Ϊ�����ͼ]
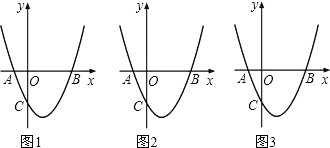
��1��k= ����A������Ϊ ����B������Ϊ ��
��2����������y=x2��2x+k�Ķ���ΪM�����ı���ABMC�������
��3����x���·������������Ƿ����һ��D��ʹ�ı���ABDC�������������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
��4����������y=x2��2x+k�����Q��ʹ��BCQ����BCΪֱ�DZߵ�ֱ�������Σ�
���𰸡���1����3������1��0������3��0������2��9��
��3�����ڵ�D��![]() ��
��![]() ����ʹ�ı���ABDC��������Ϊ
����ʹ�ı���ABDC��������Ϊ![]() ��
��
��4�����������ϴ��ڵ�Q1����2��5����Q2��1����4����ʹ��BCQ1����BCQ2����BCΪֱ�DZߵ�ֱ�������Σ�
��������
�����������1����C��0����3�����������߽���ʽ�ɵ�kֵ����y=0���ɵ�A��B����ĺ����ꣻ
��2����M����x��Ĵ��ߣ����ı���ABMC�ָ������ֱ�������κ�һ��ֱ�����Σ������ǵ�����ͣ�
��3����D��m��m2��2m��3��������OD�����ı���ABDC������ֳ���AOC����DOC����DOB������ͣ������ʽ�����ֵ����4�������ֿ��ܣ�BΪֱ�Ƕ��㡢CΪֱ�Ƕ��㣬Ҫ�����ʶ��OBC�������ԣ��ǵ���ֱ�������Σ�����ͨ����ֱ���������������߶εij��ȣ�
�⣺��1����C��0����3�����������߽���ʽy=x2��2x+k�е�k=��3
��y=x2��2x��3��
��y=0��
��x2��2x��3=0��
���x1=��1��x2=3��
��A����1��0����B��3��0����
��2����y=x2��2x��3=��x��1��2��4��
�������ߵĶ���ΪM��1����4��������OM��
����AOC�����=![]() ����MOC�����=
����MOC�����=![]() ��
��
��MOB�����=6��
���ı���ABMC�����=��AOC�����+��MOC�����+��MOB�����=9��
˵����Ҳ�ɹ���M�������ߵĶԳ��ᣬ���ı���ABMC����
��ת��Ϊ��1��������2��ֱ������������ĺͣ�
��3����ͼ��2������D��m��m2��2m��3��������OD��
��0��m��3��m2��2m��3��0
����AOC�����=![]() ����DOC�����=
����DOC�����=![]() m��
m��
��DOB�����=��![]() ��m2��2m��3����
��m2��2m��3����
���ı���ABDC�����=��AOC�����+��DOC�����+��DOB�����
=��![]() m2+
m2+![]() m+6
m+6
=��![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
�����ڵ�D��![]() ��
��![]() ����ʹ�ı���ABDC��������Ϊ
����ʹ�ı���ABDC��������Ϊ![]() ��
��
��4�������������
��ͼ��3��������B��BQ1��BC�����������ڵ�Q1����y���ڵ�E������Q1C��
�ߡ�CBO=45����
���EBO=45����BO=OE=3��
����E��������0��3����
��ֱ��BE�Ľ���ʽΪy=��x+3��
��![]()
���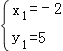
![]()
����Q1����������2��5����
��ͼ��4��������C��CF��CB�����������ڵ�Q2����x���ڵ�F������BQ2��
�ߡ�CBO=45����
���CFB=45����OF=OC=3��
����F����������3��0����
��ֱ��CF�Ľ���ʽΪy=��x��3��
��![]()
���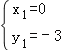
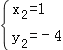
����Q2��������1����4����
���ϣ����������ϴ��ڵ�Q1����2��5����Q2��1����4����ʹ��BCQ1����BCQ2����BCΪֱ�DZߵ�ֱ�������Σ�
˵������ͼ��4������Q2�������߶���M��ֱ��֤����BCMΪֱ��������ͬ�����ԣ�




 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������ҪmԪ����һ��������ҪnԪ������4������7��������Ҫ��������
A. ��7m+4n��Ԫ B. 28mnԪ C. ��4m+7n��Ԫ D. 11mnԪ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·�߰�װ��·����֧���϶˵ĸֹ�ABCD֧�ţ�AB=25cm��CG��AF��FD��AF����G����F�ֱ��Ǵ��㣬BG=40cm��GF=7cm����ABC=120������BCD=160���������ֹ�ABCD�ij��ȣ����ֹܵ�ֱ�����Բ��ƣ������ȷ��1cm���ο����ݣ�sin10���0.17��cos10���0.98��tan10���0.18��sin20���0.34��cos20���0.94��tan20���0.36��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���M����2��3���ڣ�������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��ƽ���ı��Σ��Խ���OB��y���������ϣ�λ�ڵ�һ���ĵ�A�͵ڶ����ĵ�C�ֱ���˫����![]() ��
��![]() ��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��![]() ������Ӱ���������
������Ӱ���������![]() ��k1+k2�����۵���AOC=90��ʱ��|k1|=|k2|������OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ����ǣ� ��
��k1+k2�����۵���AOC=90��ʱ��|k1|=|k2|������OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ����ǣ� ��

A���٢ڢ� B���ڢ� C���٢ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ����( )
A. ���a>b��b>c����a>c
B. ��a>b����ac>bc
C. ����AOB����BOC�������������ǶԶ���
D. ������ǵĺ͵���180�㣬��ô�������ǻ�Ϊ�ڲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
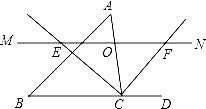
��1����CE=12��CF=5����OC�ij���
��2������O�ڱ�AC���˶�ʱ���ı���BCFE�������������ǣ���֤���������ǣ���˵�����ɣ�
��3������O�˶����δ����ҡ�ABC����ʲô����ʱ���ı���AECF�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı��ε������Խ��߳���8cm��16cm�������ƽ���ı��ε�һ�߳������ǣ�������
A. 3cm B. 4cm C. 8cm D. 12cm
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com