
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连结EFBF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
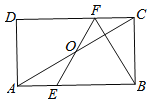
(1)求证:OE=OF;(2)若BC=3![]() ,求AB的长
,求AB的长
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据矩形的对边平行可得AB∥CD,再根据两直线平行,内错角相等求出∠BAC=∠FCO,然后利用“角角边”证明△AOE和△COF全等,再根据全等三角形的即可得证;
(2)连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC,再利用勾股定理列式计算即可求出AB.
(1)证明:在矩形ABCD中,AB∥CD,
∴∠BAC=∠FCO,
在△AOE和△COF中,
 ,
,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:如图,连接OB,

∵BE=BF,OE=OF,
∴BO⊥EF,
∴在Rt△BEO中,∠BEF+∠ABO=90°,
由直角三角形斜边上的中线等于斜边上的一半可知:OA=OB=OC,
∴∠BAC=∠ABO,
又∵∠BEF=2∠BAC,
即2∠BAC+∠BAC=90°,
解得∠BAC=30°,
∵BC=2![]() ,
,
∴AC=2BC=4![]() ,
,
∴AB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示.线段AB、DC分别表示甲、乙两座建筑物的高.AB⊥BC,DC⊥BC,两建筑物间距离BC=30米,若甲建筑物高AB=28米,在A点测得D点的仰角α=45°,则乙建筑物高DC=______米.
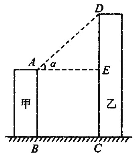
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
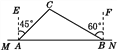
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图、在平行四边形ABCD中,E、F是对角线BD上的两点,则下列条件中不能判定四边形AECF是平行四边形的是( )

A.BD=DFB.AF![]() BD,
BD,![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
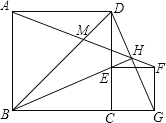
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(-1,0),点B(-3,0),且OB=OC,
轴交于点A(-1,0),点B(-3,0),且OB=OC,
(1)求抛物线的解析式;
(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;
(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值.
②点D关于点E的对称点为F.当m为何值时,四边形MDNF为矩形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组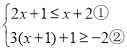 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得____________________;
(Ⅱ)解不等式②,得_______________________;
(III)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com