解:(1)AB=AC时,原证明成立.
(2)AB>AC时
如图2所示:
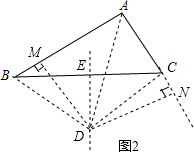
三条线段AB、AC、BE的等量关系为AB=AC+2BM,理由如下:
∵AD为∠BAC的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△ADM和Rt△ADN中,
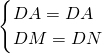
,
∴Rt△DMB≌Rt△DMC(HL),
∴AM=AN,
又OE为BC的垂直平分线,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
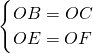
,
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN,
则AB=AM+BM=AN+BM=AC+CN+BM=AC+2BM;
(3)AC=AB+2BM
∵AD为∠BAC的平分线,DM⊥AB,DN⊥AC,
∴DM=DN,
在Rt△ADM和Rt△ADN中,
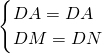
,
∴Rt△DMB≌Rt△DMC(HL),
∴AM=AN,
又OE为BC的垂直平分线,
∴DB=DC,
在Rt△DMB和Rt△DNC中,
,
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN,
则AC=AN+CN=AM+CN=AB+CN+BM=AC+2BM;
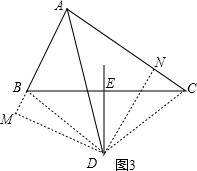
分析:(1)当AB=AC时,解答正确;
(2)AB>AC时,根据题意画出相应的图形,三条线段AB、AC、BE的等量关系为AB=AC+2BM,理由为:由AD为角平分线,DM垂直于AB,DN垂直于AC,利用角平分线定理得到DM=DN,再由AD为公共边,利用HL得到直角三角形ADM与直角三角形ADN全等,由全等三角形的对应边相等得到M=AN,再由DE为线段BC的垂直平分线,利用线段垂直平分线定理得到DB=DC,利用HL得出直角三角形DBM与直角三角形DNC全等,由全等三角形的对应边相等得到BM=CN,等量代换可得证.
(3)AB<AC时,根据题意画出相应的图形,三条线段AB、AC、BE的等量关系为AC=AB+2BM,理由为:由AD为角平分线,DM垂直于AB,DN垂直于AC,利用角平分线定理得到DM=DN,再由AD为公共边,利用HL得到直角三角形ADM与直角三角形ADN全等,由全等三角形的对应边相等得到M=AN,再由DE为线段BC的垂直平分线,利用线段垂直平分线定理得到DB=DC,利用HL得出直角三角形DBM与直角三角形DNC全等,由全等三角形的对应边相等得到BM=CN,等量代换可得证.
点评:本题考查了全等三角形的判定与性质的运用,角平分线定理的运用,以及线段垂直平分线定理的运用,全等三角形的判定方法有:SSS;ASA;AAS;SAS,以及HL(直角三角形判定全等的方法)解答时证明三角形全等是关键.

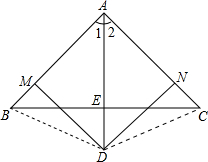 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形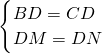 ∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.又∵AM=AN,∴AB=AC,∴△ABC一定是等腰三角形.你认为对吗?
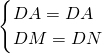 ,
,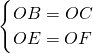 ,
,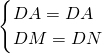 ,
,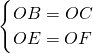 ,
,


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案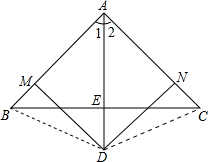 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形