
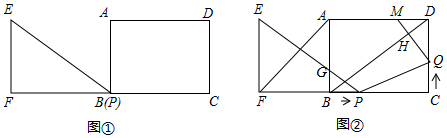
���� ��1����ͼ1�У���PQ��BDʱ��$\frac{CQ}{CD}$=$\frac{CP}{CB}$���ɵ�$\frac{t}{6}$=$\frac{8-t}{8}$���ⷽ�̼��ɣ�
��2����ͼ2�У���0��t��6ʱ��S�����AFPQM=S����AFCD-S��DMQ-S��PQC���ɴ˼��㼴�ɽ�����⣻
��3��������ڣ����������г����̼��ɽ�����⣻
��4����ͼ3�У�����MG��MP����MK��BC��K�����ù��ɶ���������MG=MP���г����̼��ɽ�����⣻
��� �⣺��1����ͼ1�У�
��PQ��BDʱ��$\frac{CQ}{CD}$=$\frac{CP}{CB}$��
��$\frac{t}{6}$=$\frac{8-t}{8}$��
��t=$\frac{24}{7}$��
��t=$\frac{24}{7}$sʱ��PQ��BD��
��2����ͼ2�У�
��0��t��6ʱ��S�����AFPQM=S����AFCD-S��DMQ-S��PQC
=$\frac{1}{2}$��8+8-t+8��•6-$\frac{1}{2}$•��6-t��•$\frac{3}{4}$��6-t��-$\frac{1}{2}$•��8-t��•t
=$\frac{1}{8}$t2-$\frac{5}{2}$t+$\frac{117}{2}$��
��3����ͼ2�У�������ڣ����У�$\frac{1}{8}$t2-$\frac{5}{2}$t+$\frac{117}{2}$������48=9��8��
���t=2��18����������
��t=2sʱ��S�����AFPQM��S����ABCD=9��8��
��4�����ڣ�
���ɣ���ͼ3�У�����MG��MP����MK��BC��K��
��֪��AG=6-$\frac{3}{4}$t��DQ=6-t��DM=KC=$\frac{3}{4}$��6-t����PK=8-t-$\frac{3}{4}$��6-t����MK=CD=6��
�ߵ�M��PG�Ĵ�ֱƽ�����ϣ�
��MG=MP��
��AG2+AM2=PK2+MK2��
�ࣨ6-$\frac{3}{4}$t��2+[8-$\frac{3}{4}$��6-t��]2=62+[8-t-$\frac{3}{4}$��6-t��]2��
���t=$\frac{32}{17}$��0����������
��t=$\frac{32}{17}$sʱ����M���߶�PG�Ĵ�ֱƽ������
���� ���⿼���ı����ۺ��⡢ƽ���߷��߶γɱ������������ɶ���������ε������֪ʶ������Ĺؼ���ѧ�����÷ָ�����������ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
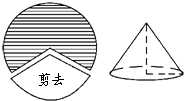 ��ͼ�����뾶Ϊ15cm��Բ��ֽƬ��ȥ$\frac{2}{5}$Բ�ܵ�һ�����Σ���ʣ�µ�����Χ��һ��Բ�IJ��棨�ӷ���Բ��ƣ������Բ�ĸ��ǣ�������
��ͼ�����뾶Ϊ15cm��Բ��ֽƬ��ȥ$\frac{2}{5}$Բ�ܵ�һ�����Σ���ʣ�µ�����Χ��һ��Բ�IJ��棨�ӷ���Բ��ƣ������Բ�ĸ��ǣ�������| A�� | 12cm | B�� | 8cm | C�� | 20cm | D�� | 18cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -m | B�� | -1 | C�� | $\frac{3}{4}$ | D�� | -$\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
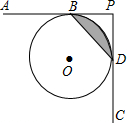 ��ͼ��ֱ��AB��CD�ֱ����O������B��D���㣬��AB��CD������ΪP������BD����BD=4������Ӱ���ֵ����Ϊ2��-4��
��ͼ��ֱ��AB��CD�ֱ����O������B��D���㣬��AB��CD������ΪP������BD����BD=4������Ӱ���ֵ����Ϊ2��-4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
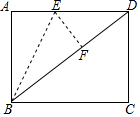 ��ͼ���ھ���ABCD��BC=8��CD=6������ABE��BE�۵���ʹ��Aǡ�����ڶԽ���BD��F������DE�ij��ǣ�������
��ͼ���ھ���ABCD��BC=8��CD=6������ABE��BE�۵���ʹ��Aǡ�����ڶԽ���BD��F������DE�ij��ǣ�������| A�� | 3 | B�� | $\frac{24}{5}$ | C�� | 5 | D�� | $\frac{89}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com