
 我县甲、乙两家甜橘柚基地生产的甜橘柚品质相同,销售价格也相同.“元旦”期间,两家均推出了优惠方案,甲基地的优惠方案是:每个游客进园需购买门票,采摘的甜橘柚打六折优惠;乙基地的优惠方案是:每个游客进园不需购买门票,采摘园的甜橘柚超过10千克后,超过部分打五折优惠.优惠期间,设某游客的甜橘柚采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中射线AB表示y1与x之间的函数关系.
我县甲、乙两家甜橘柚基地生产的甜橘柚品质相同,销售价格也相同.“元旦”期间,两家均推出了优惠方案,甲基地的优惠方案是:每个游客进园需购买门票,采摘的甜橘柚打六折优惠;乙基地的优惠方案是:每个游客进园不需购买门票,采摘园的甜橘柚超过10千克后,超过部分打五折优惠.优惠期间,设某游客的甜橘柚采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中射线AB表示y1与x之间的函数关系.分析 (1)根据函数图象可以求得甜橘柚销售价格是每千克的钱数和甲基地的门票;
(2)根据题意和函数图象可以分别求得y1、y2与x的函数表达式;
(3)根据(2)中y2与x的函数表达式可以解答本题.
解答 解:(1)由题意可得,
甜橘柚销售价格是每千克:(230-50)÷10÷0.6=30(元),甲基地的门票是50元/人,
故答案为:30,50;
(2)由题意可得,
y1=50+30x×0.6=18x+50,
当0<x≤10时,y2=30x,
当x>10时,y2=30×10+(x-10)×30×0.5=15x+150,
即y1=18x+50,y2=$\left\{\begin{array}{l}{30x}&{(0<x≤10)}\\{15x+150}&{(x>10)}\end{array}\right.$;
(3)y2与x的函数图象如右图所示,
当0<x≤10时,
18x+50<30x,
解得,x>$6\frac{1}{4}$,
∴当6$\frac{1}{4}$<x≤10时,采摘相同量时选择甲基地所需总费用较少;
当x>10时,
18x+50<15x+150,
解得,x$<33\frac{1}{3}$,
即当10<x<$33\frac{1}{3}$时,采摘相同量时选择甲基地所需总费用较少;
由上可得,当6$\frac{1}{4}$<x<$33\frac{1}{3}$时,采摘相同量时选择甲基地所需总费用较少.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合和函数的思想解答问题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
 如图,点D是等边三角形ABC的边AC上一点,DE∥BC交AB于E,延长CB至F,使BF=AD,连结DF交BE于G.
如图,点D是等边三角形ABC的边AC上一点,DE∥BC交AB于E,延长CB至F,使BF=AD,连结DF交BE于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
如图,△ABC中,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
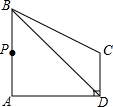 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com