
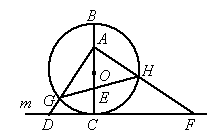
(2006,宜昌)如图,⊙O的直径BC=4,过点C作⊙O的切线m,D是直线m上一点,且DC=2,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AD的垂线交直线m于点F,交⊙O于点H,连结GH交BC于点E.
(1)当A是BO的中点时,求AF的长;
(2)若∠AGH=∠AFD,求△AGH的面积.
|
解: (1)∵BC=4,A是OB的中点,∴AC=3.又∵ DC为⊙O的切线,∴∠ ACD=∠ACF=90°.∵ AD⊥AF,∴∠ ADC、∠CAF都与∠DAC互余,∴∠ ADC=∠FAC,∴△ ACD∽△FCA,∴ CD∶AC=CA∶FC.解得 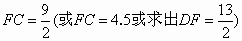 . .
(2) ∵∠AGH=∠AFD,∠DAF=∠HAG=90°,∴△ AGH∽△AFD,∴∠ AGH=∠F=∠CAG,∠AHG=∠D=∠CAF,∴ AE=CE=HE(或AE是Rt△AGH斜边GH上的中线).根据垂径定理推论: GH⊥BC,∴可知 GH是⊙O的直径或GH是垂直于直径的弦.①如图 (1),如果GH是直径,此时A、B两点重合,GH=4,而DF=10,∴△AGH与△AFD的相似比为2∶5,∴△ AGH与△AFD的面积比为4∶25.而△ AFD面积为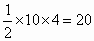 , ,
∴△ AGH面积为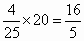 (或3.2). (或3.2).
②如图 (2),如果GH不是直径,则GH⊥BC,∴ AC垂直平分GH,AG=AH,∴GH∥DF.而∠ GAH=90°,∴∠AGH=45°,∴∠ D=∠AGH=45°.在 Rt△ACD中,∠DAC=45°,∴AC=DC=2,而OC=2,∴ A、O两点重合,那么AG=AH=2.∴△ AGH面积为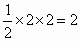 . . |


科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年天津市中考数学模拟试卷(3)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年湖北省宜昌市中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年湖北省宜昌市中考数学试卷(大纲卷)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年湖北省宜昌市中考数学试卷(课标卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com