

| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:不详 题型:解答题
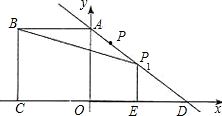 形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
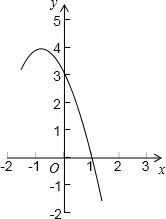
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 5 |
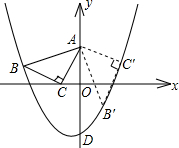 中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.
),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
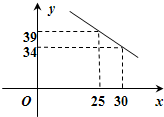 4万元,且所有资金全部用于生产这三种型号的汽车,三种型号的汽车生产成本和售价如下表:
4万元,且所有资金全部用于生产这三种型号的汽车,三种型号的汽车生产成本和售价如下表:| A | B | C | |
| 成本(万元/辆) | 12 | 15 | 18 |
| 售价(万元/辆) | 14 | 18 | 22 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.41 | B.42 | C.42.5 | D.43 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com