
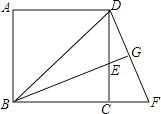
【题目】如图,有一块正方形![]() ,小王连接对角线
,小王连接对角线![]() 后,作
后,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,又将
,又将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 后到
后到![]() 的位置,并延长
的位置,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】某商店要运一批货物,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完这批货物,则乙车所运趟数是甲车的2倍;已知乙车毎趟运费比甲车少200元.
(1)分别求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此批货物,需运多少趟;
(3)若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此批货物,其中x、y均为正整数,设总运费为w(元),求w与x的函数关系式,直接写出w的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
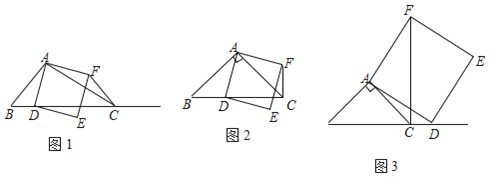
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
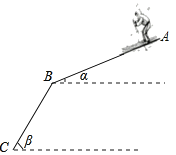
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线______;
(2)当AB=2时,求抛物线M的函数表达式以及顶点D的坐标;
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3<4),若当-2≤n≤-1时,总有x1-x3<x3-x2<0,请结合函数的图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润![]() (单位:元)与售价
(单位:元)与售价![]() (单位:元/千克)之间的函数关系式.
(单位:元/千克)之间的函数关系式.
(2)商场将在月销售成本不超过3000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
(3)当售价定为多少元时,会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是AB边的中点,点E为AC中点,点F在边BC上,AF交DE于点G,点H是FC的中点,连接GH.

(1)如图1,求证:四边形GHCE是平行四边形;
(2)如图2,当AB=AC,点F是BC中点时,在不添加任何辅助线的情况下,请直接写出图中所有长度等于![]() BF的线段.
BF的线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com