
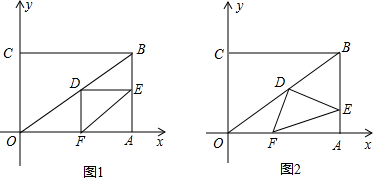
分析 (1)当t=3时,点E为AB的中点,由三角形中位线定理得出DE∥OA,DE=$\frac{1}{2}$OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
(2)作DM⊥OA于M,DN⊥AB于N,证明四边形DMAN是矩形,得出∠MDN=90°,DM∥AB,DN∥OA,由平行线得出比例式$\frac{BD}{DO}=\frac{BN}{NA}$,$\frac{DO}{BD}$=$\frac{OM}{MA}$,由三角形中位线定理得出DM=$\frac{1}{2}$AB=3,DN=$\frac{1}{2}$OA=4,证明△DMF∽△DNE,得出$\frac{DF}{DE}=\frac{DM}{DN}$=$\frac{3}{4}$,再由三角函数定义即可得出答案;
(3)作作DM⊥OA于M,DN⊥AB于N,若AD将△DEF的面积分成1:2的两部分,设AD交EF于点G,则点G为EF的三等分点;
①当点E到达中点之前时,NE=3-t,由△DMF∽△DNE得:MF=$\frac{3}{4}$(3-t),求出AF=4+MF=-$\frac{3}{4}$t+$\frac{25}{4}$,得出G($\frac{3t+71}{12}$,$\frac{2}{3}$t),求出直线AD的解析式为y=-$\frac{3}{4}$x+6,把G($\frac{3t+71}{12}$,$\frac{2}{3}$t)代入即可求出t的值;
②当点E越过中点之后,NE=t-3,由△DMF∽△DNE得:MF=$\frac{3}{4}$(t-3),求出AF=4-MF=-$\frac{3}{4}$t+$\frac{25}{4}$,得出G($\frac{3t+23}{6}$,$\frac{1}{3}$t),代入直线AD的解析式y=-$\frac{3}{4}$x+6求出t的值即可.
解答 解:(1)当t=3时,点E为AB的中点,
∵A(8,0),C(0,6),
∴OA=8,OC=6,
∵点D为OB的中点,
∴DE∥OA,DE=$\frac{1}{2}$OA=4,
∵四边形OABC是矩形,
∴OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°,
∴四边形DFAE是矩形,
∴DF=AE=3;
(2)∠DEF的大小不变;理由如下: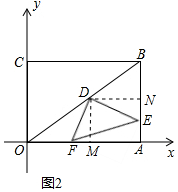
作DM⊥OA于M,DN⊥AB于N,如图2所示:
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM∥AB,DN∥OA,
∴$\frac{BD}{DO}=\frac{BN}{NA}$,$\frac{DO}{BD}$=$\frac{OM}{MA}$,
∵点D为OB的中点,
∴M、N分别是OA、AB的中点,
∴DM=$\frac{1}{2}$AB=3,DN=$\frac{1}{2}$OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN,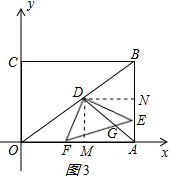
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE,
∴$\frac{DF}{DE}=\frac{DM}{DN}$=$\frac{3}{4}$,
∵∠EDF=90°,
∴tan∠DEF=$\frac{DF}{DE}$=$\frac{3}{4}$;
(3)作DM⊥OA于M,DN⊥AB于N,
若AD将△DEF的面积分成1:2的两部分,
设AD交EF于点G,则点G为EF的三等分点;
①当点E到达中点之前时,如图3所示,NE=3-t,
由△DMF∽△DNE得:MF=$\frac{3}{4}$(3-t),
∴AF=4+MF=-$\frac{3}{4}$t+$\frac{25}{4}$,
∵点G为EF的三等分点,
∴G($\frac{3t+71}{12}$,$\frac{2}{3}$t),
设直线AD的解析式为y=kx+b,
把A(8,0),D(4,3)代入得:$\left\{\begin{array}{l}{8k+b=0}\\{4k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$,
∴直线AD的解析式为y=-$\frac{3}{4}$x+6,
把G($\frac{3t+71}{12}$,$\frac{2}{3}$t)代入得:t=$\frac{75}{41}$;
②当点E越过中点之后,如图4所示,NE=t-3,
由△DMF∽△DNE得:MF=$\frac{3}{4}$(t-3),
∴AF=4-MF=-$\frac{3}{4}$t+$\frac{25}{4}$,
∵点G为EF的三等分点,
∴G($\frac{3t+23}{6}$,$\frac{1}{3}$t),
代入直线AD的解析式y=-$\frac{3}{4}$x+6得:t=$\frac{75}{17}$;
综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为$\frac{75}{41}$或$\frac{75}{17}$
点评 本题是四边形综合题目,考查了矩形的性质、坐标与图形性质、三角形中位线定理、相似三角形的判定与性质、平行线分线段成比例定理、一次函数解析式的求法等知识;本题综合性强,难度较大.


科目:初中数学 来源: 题型:选择题
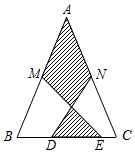 如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.
如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连结DN,EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分面积为( )cm2.| A. | 25 | B. | 35 | C. | 30 | D. | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
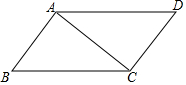 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码(码) | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 5 | 10 | 2 | 1 |
| A. | 35码,35码 | B. | 35码,36码 | C. | 36码,35码 | D. | 36码,36码 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
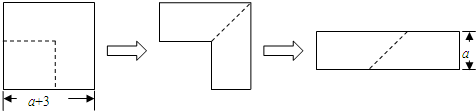
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+$\frac{12}{MA•DN}$的最小值为2$\sqrt{3}$.
将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+$\frac{12}{MA•DN}$的最小值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
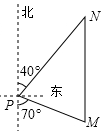 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )| A. | 40海里 | B. | 60海里 | C. | 70海里 | D. | 80海里 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com