
在平面直角坐标系中,现将一块等腰直角三角形ABC放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示;抛物线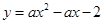 经过点B。
经过点B。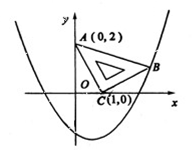
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,求所以点P的坐标;若不存在,请说明理由。
解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO="90°" ,∠ACO+∠OAC =90°;
∴∠BCD=∠CAO; 又∵∠BDC=∠COA=90°;CB=AC,
∴△BDC≌△CAO=90°,∴BD=OC=1,CD=OA=2;∴点B的坐标为(3,1)
(2)抛物线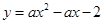 经过点B(3,1),则得
经过点B(3,1),则得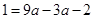 解得
解得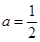 ,所以抛物线的解析式为
,所以抛物线的解析式为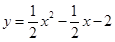
(3)假设存在点P,似的△ACP是直角三角形:
①若以AC为直角边,点C为直角顶点;则延长BC至点P1 使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,如图1。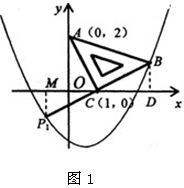
∵CP1=BC,∠MCP1=∠BCD, ∠P1MC=∠BDC=90°,∴△MCP1≌△BCD
∴ CM=CD=2,P1M=BD=1,可求得点P1(-1,-1);经检验点P1(-1,-1)在抛物线为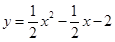 上;
上;
②若以AC为直角边, 点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,如图2。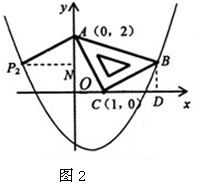
同理可得△AP2N≌△CAO;∴NP2=OA=2,AN=OC=1,可求得点P2(-2,1),;经检验点P2(-2,1)也在抛物线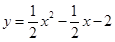 上;
上;
③若以AC为直角边, 点A为直角顶点;则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,如图3。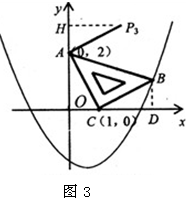
同理可得△AP3H≌△CAO;∴HP3=OA=2,AH=OC=1,可求得点P3(2,3),;经检验点P3(2,3)不抛物线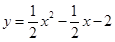 上;
上;
故符合条件的点有P1(-1,-1),P2(-2,1)两个。
解析


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com