
”¾ĢāÄæ”æČēĶ¼£¬ŹżÖįÉĻÓŠČżøöµćA”¢B”¢C£¬±ķŹ¾µÄŹż·Ö±šŹĒ©4”¢©2”¢3£¬Ēė»Ų“š£ŗ
£Ø1£©ČōŹ¹C”¢BĮ½µćµÄ¾ąĄėÓėA”¢BĮ½µćµÄ¾ąĄėĻąµČ£¬ŌņŠč½«µćCĻņ×óŅʶÆ_____øöµ„Ī»£»
£Ø2£©µćA”¢B”¢CæŖŹ¼ŌŚŹżÖįÉĻŌĖ¶Æ£¬ČōµćAŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬Ķ¬Ź±£¬µćBŗĶµćC·Ö±šŅŌĆæĆė2øöµ„Ī»³¤¶ČŗĶ5øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌĖ¶Æ£¬ŌĖ¶ÆtĆėÖÓ¹żŗó£ŗ
¢ŁµćA”¢B”¢C±ķŹ¾µÄŹż·Ö±šŹĒ_____”¢_____”¢_____ £ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©£»
¢ŚČōµćBÓėµćCÖ®¼äµÄ¾ąĄė±ķŹ¾ĪŖd1£¬µćAÓėµćBÖ®¼äµÄ¾ąĄė±ķŹ¾ĪŖd2£®ŹŌĪŹ£ŗd1©d2µÄÖµŹĒ·ńĖę×ÅŹ±¼ätµÄ±ä»Æ¶ųøıä£æČō±ä»Æ£¬ĒėĖµĆ÷ĄķÓÉ£»Čō²»±ä£¬ĒėĒó³öd1©d2Öµ£®
![]()
”¾“š°ø”æ 3»ņ7 ©4©t ©2+2t ©2+2t
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉAB=2£¬½įŗĻŹżÖį¼“æÉµĆ³öµćCĻņ×óŅĘ¶ÆµÄ¾ąĄė£»
£Ø2£©¢Ł½įŗĻĀ·³Ģ=Ź±¼ä”ĮĖŁ¶ČŠ“³ö“š°ø£»
¢ŚĻČĒó³öd1=3t+5£¬d2=3t+2£¬“Ó¶ųµĆ³öd1©d2=2£®
ŹŌĢā½āĪö£ŗ£Ø1£©ÓŠŹżÖįæÉÖŖ£ŗA”¢BĮ½µćµÄ¾ąĄėĪŖ2£¬Bµć”¢Cµć±ķŹ¾µÄŹż·Ö±šĪŖ£ŗ©2”¢3£¬
ĖłŅŌµ±C”¢BĮ½µćµÄ¾ąĄėÓėA”¢BĮ½µćµÄ¾ąĄėĻąµČŹ±£¬Šč½«µćCĻņ×óŅʶÆ3øö»ņ7øöµ„Ī»£»
¹Ź“š°øŹĒ£ŗ3»ņ7£»
£Ø2£©¢ŁµćA±ķŹ¾µÄŹżŹĒ©4©t£»µćB±ķŹ¾µÄŹżŹĒ©2+2t£»µćCĖł±ķŹ¾µÄŹżŹĒ3+5t£®
¹Ź“š°øŹĒ£ŗ©4©t£»©2+2t£»3+5t£»
¢Śd1©d2µÄÖµ²»Ėę×ÅŹ±¼ätµÄ±ä»Æ¶ųøı䣬ĘäÖµŹĒ3£¬ĄķÓÉČēĻĀ£ŗ
”ßµćA¶¼ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬µćBŗĶµćC·Ö±šŅŌĆæĆė2øöµ„Ī»³¤¶ČŗĶ5øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÓŅŌĖ¶Æ£¬
”ąd1=3t+5£¬d2=3t+2£¬
”ąd1©d2=£Ø3t+5£©©£Ø3t+2£©=3£®


 Ņ»ÅµŹéŅµŹī¼Ł×÷ŅµæģĄÖ¼ŁĘŚŌĘÄĻĆĄŹõ³ö°ęÉēĻµĮŠ“š°ø
Ņ»ÅµŹéŅµŹī¼Ł×÷ŅµæģĄÖ¼ŁĘŚŌĘÄĻĆĄŹõ³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£ŗEŌŚ”÷ABCµÄAC±ßµÄŃÓ³¤ĻßÉĻ£¬DµćŌŚAB±ßÉĻ£¬DE½»BCÓŚµćF£¬DF=EF£¬BD=CE.ĒóÖ¤£ŗ”÷ABCŹĒµČŃüČż½ĒŠĪ£®£Ø¹żD×÷DG”ĪAC½»BCÓŚG£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼AB”ĪCD£®”Ļ1=”Ļ2£¬”Ļ3=”Ļ4£¬ŹŌĖµĆ÷AD”ĪBE£®

½ā£ŗ”ßAB”ĪCD£ØŅŃÖŖ£©
”ą”Ļ4=”Ļ £Ø £©
”ß”Ļ3=”Ļ4£ØŅŃÖŖ£©
”ą”Ļ3=”Ļ £Ø £©
”ß”Ļ1=”Ļ2£ØŅŃÖŖ£©
”ą”Ļ1+”ĻCAF=”Ļ2+”ĻCAF£Ø
¼“”Ļ =”Ļ £Ø £©
”ą”Ļ3=”Ļ
”ąAD”ĪBE£Ø £©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĆęŹĒijĶ¬Ń§¶Ō¶ąĻīŹ½£Øx2£4x+2£©£Øx2£4x+6£©+4½ųŠŠŅņŹ½·Ö½āµÄ¹ż³Ģ£®
½ā£ŗÉčx2£4x=y
ŌŹ½=£Øy+2£©£Øy+6£©+4 £ØµŚŅ»²½£©
=y2+8y+16 £ØµŚ¶ž²½£©
=£Øy+4£©2£ØµŚČż²½£©
=£Øx2£4x+4£©2£ØµŚĖIJ½£©
»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©øĆĶ¬Ń§µŚ¶ž²½µ½µŚČż²½ŌĖÓĆĮĖŅņŹ½·Ö½āµÄ_______£®
A£®ĢįČ”¹«ŅņŹ½ |
B£®Ę½·½²ī¹«Ź½ |
C£®Į½ŹżŗĶµÄĶźČ«Ę½·½¹«Ź½ |
D£®Į½Źż²īµÄĶźČ«Ę½·½¹«Ź½ |
£Ø2£©øĆĶ¬Ń§ŅņŹ½·Ö½āµÄ½į¹ūŹĒ·ń³¹µ×£æ________£®£ØĢī”°³¹µ×”±»ņ”°²»³¹µ×”±£©Čō²»³¹µ×£¬ĒėÖ±½ÓŠ“³öŅņŹ½·Ö½āµÄ×īŗó½į¹ū_________ £®
£Ø3£©ĒėÄćÄ£·ĀŅŌÉĻ·½·Ø³¢ŹŌ¶Ō¶ąĻīŹ½£Øx2£2x£©£Øx2£2x+2£©+1½ųŠŠŅņŹ½·Ö½ā£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
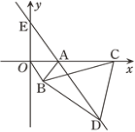
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAµÄ×ų±źĪŖ(1£¬0)£¬ŅŌĻ߶ĪOAĪŖ±ßŌŚµŚĖÄĻóĻŽÄŚ×÷µČ±ßČż½ĒŠĪ”÷AOB£¬µćCĪŖxÕż°ėÖįÉĻŅ»¶Æµć(OC£¾1)£¬Į¬½ÓBC£¬ŅŌĻ߶ĪBCĪŖ±ßŌŚµŚĖÄĻóĻŽÄŚ×÷µČ±ßČż½ĒŠĪ”÷CBD£¬Į¬½ÓDA²¢ŃÓ³¤£¬½»yÖįÓŚµćE.
(1)ĒóÖ¤£ŗ”÷OBC”Õ”÷ABD
(2)ŌŚµćCµÄŌĖ¶Æ¹ż³ĢÖŠ£¬”ĻCADµÄ¶ČŹżŹĒ·ń»į±ä»Æ£æČē¹ū²»±ä£¬ĒėĒó³ö”ĻCADµÄ¶ČŹż;Čē¹ū±ä»Æ£¬ĒėĖµĆ÷ĄķÓÉ.
(3)µ±µćCŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬ŅŌA£¬E£¬CĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬OŹĒ¾ŲŠĪABCDµÄ¶Ō½ĒĻߵĽ»µć£¬E£¬F£¬G£¬H·Ö±šŹĒOA£¬OB£¬OC£¬ODÉĻµÄµć£¬ĒŅAE£½BF£½CG£½DH.
(1)ĒóÖ¤£ŗĖıߊĪEFGHŹĒ¾ŲŠĪ£»
(2)ČōE£¬F£¬G£¬H·Ö±šŹĒOA£¬OB£¬OC£¬ODµÄÖŠµć£¬ĒŅDG”ĶAC£¬OF£½2cm£¬Ēó¾ŲŠĪABCDµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĪŽĀŪkČ”ŗĪŹµŹż£¬Ö±Ļßy=(k£1)x+4£5k×ܾ¹ż¶ØµćP£¬ŌņµćPÓė¶ÆµćQ(5m-1£¬5m+1)µÄ¾ąĄėµÄ×īŠ”ÖµĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»“ĪŹżŃ§»ī¶ÆæĪÉĻ£¬ĄĻŹ¦“ųĮģѧɜȄ²āŅ»ĢõÄĻ±±Į÷ĻņµÄŗÓæķ£¬ČēĶ¼ĖłŹ¾£¬Ä³Ń§ÉśŌŚŗÓ¶«°¶µćA“¦¹Ū²āµ½ŗÓ¶Ō°¶Ė®±ßÓŠŅ»µćC£¬²āµĆCŌŚA±±Ę«Ī÷31”ćµÄ·½ĻņÉĻ£¬ŃŲŗÓ°¶Ļņ±±Ē°ŠŠ40Ć×µ½“ļB“¦£¬²āµĆCŌŚB±±Ę«Ī÷45”ćµÄ·½ĻņÉĻ£¬ĒėÄćøł¾ŻŅŌÉĻŹż¾Ż£¬ĒóÕāĢõŗÓµÄæķ¶Č£®£Ø²Īæ¼ŹżÖµ£ŗtan31”ć”Ö ![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĪŖĮĖ²āĮæijµēĻßøĖ£Øµ×²ææɵ½“ļ£©µÄøß¶Č£¬×¼±øĮĖČēĻĀµÄ²āĮ湤¾ß£ŗ
¢ŁĘ½Ćę¾µ£»¢ŚĘ¤³ß£»¢Ū³¤ĪŖ2Ć׵ıźøĖ£»¢ÜøßĪŖ1.5mµÄ²ā½ĒŅĒ£Ø²āĮæŃö½Ē”¢ø©½ĒµÄŅĒĘ÷£©£¬Ēėøł¾ŻÄćĖłÉč¼ĘµÄ²āĮæ·½°ø£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©»³öÄćµÄ²āĮæ·½°øŹ¾ŅāĶ¼£¬²¢øł¾ŻÄćµÄ²āĮæ·½°øŠ“³öÄćĖłŃ”ÓĆµÄ²āĮ湤¾ß£»
£Ø2£©½įŗĻÄćµÄŹ¾ŅāĶ¼£¬Š“³öĒóµēĻßøĖø߶ȵÄĖ¼Ā·£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com