【题目】计算：6sin60°﹣（ 
）﹣2﹣ 
+|2﹣ 
|．
【答案】解：6sin60°﹣（ 
）﹣2﹣ 
+|2﹣ 
| =6× 
﹣9﹣2 +2﹣
=3 ﹣9﹣2 +2﹣
=﹣7
【解析】首先计算乘方和开方，然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可．
【考点精析】关于本题考查的整数指数幂的运算性质和特殊角的三角函数值，需要了解aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”才能得出正确答案．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，直线l与⊙O相离，过点O作OA⊥l，垂足为A，OA交⊙O于点B，点C在直线l上，连接CB并延长交⊙O于点D，在直线l上另取一点P，使∠PCD=∠PDC．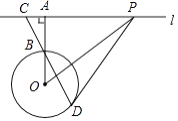 
（1）求证：PD是⊙O的切线；
（2）若AC=1，AB=2，PD=6，求⊙O的半径r和△PCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填空，完成下列说理过程
如图，∠AOB＝90°，∠COD＝90°，OA平分∠DOE，若∠BOC＝20°，求∠COE的度数
解：因为∠AOB＝90°．
所以∠BOC+∠AOC＝90°
因为∠COD＝90°
所以∠AOD+∠AOC＝90°．
所以∠BOC＝∠AOD． （ ）
因为∠BOC＝20°．
所以∠AOD＝20°．
因为OA平分∠DOE
所以∠ ＝2∠AOD＝ °． （ ）
所以∠COE＝∠COD﹣∠DOE＝ °
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列例题
解方程：|x|+|2x﹣1|＝5．
解：①当x≥0.5时，原方程可化为：x+2x﹣1＝5，它的解是x＝2；
②当0≤x＜0.5时，原方程可化为：x﹣2x+1＝5，解之，得x＝﹣4，
经检验x不合题意，舍去．
③当x＜0时，原方程可化为：﹣x﹣2x+1＝5，它的解是x＝﹣
．
所以原方程的解是x＝2或x＝﹣．
（1）根据上面的解题过程，写出方程2|x﹣1|﹣x＝4的解．
（2）根据上面的解题过程，解方程：2|x﹣1|﹣|x|＝4．
（3）方程|x|﹣2|x﹣1|＝4是否有解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角∠A是120°，第二次拐的角∠B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C的大小是( )
A. 150° B. 130° C. 140° D. 120°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥EF，则∠A、∠C、∠D、∠E满足的数量关系是（ ）
A. ∠A＋∠C＋∠D＋∠E＝360°
B. ∠A＋∠D＝∠C＋∠E
C. ∠A－∠C＋∠D＋∠E＝180°
D. ∠E－∠C＋∠D－∠A＝90°
查看答案和解析>>
科目：初中数学 来源： 题型：
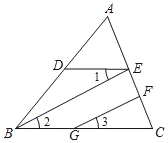
【题目】已知：如图，BE∥GF，∠1＝∠3，∠DBC＝70°，求∠EDB的大小．
阅读下面的解答过程，并填空(理由或数学式)
解：∵BE∥GF(已知)
∴∠2＝∠3( )
∵∠1＝∠3( )
∴∠1＝( )( )
∴DE∥( )( )
∴∠EDB+∠DBC＝180°( )
∴∠EDB＝180°﹣∠DBC(等式性质)
∵∠DBC＝( )(已知)
∴∠EDB＝180°﹣70°＝110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
