练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    　　如图，Rt△ABO的顶点A是双曲线与直线在第二象限的交点，AB⊥轴于B，且。求这两个函数的解析式。

     

    答案：
    解析：

    		答案：解：设点A坐标为（x，y），由，可得，

    因为，，，所以，两函数解析式分别为：，。

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

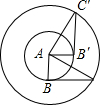    精英家教网如图，Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的，其中AB=1，BC=2，则旋转过程中弧CC′的长为（　　）
    A、
    		5
    2
    π
    B、
    5
    2
    π
    C、5π
    D、
    		5
    π

    查看答案和解析>>

    科目：初中数学 来源：非常讲解·教材全解全析　数学　七年级下　（配北师大课标） 北师大课标 题型：022

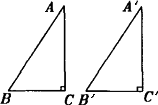
    　　如图，在△ABC和△中，∠C＝∠＝90°．

    　　①∵AB＝，BC＝(已知)，

    　　∴Rt△ABC≌△Rt△(　　)．

    　　②∵AB＝，AC＝(已知)，

    　　∴Rt△ABC≌Rt△(　　)．

    　　③∵AC＝，BC＝(已知)，

    　　∴Rt△ABC≌Rt△(　　)．

    　　④∵∠A＝∠，AB＝(已知)，

    　　∴Rt△ABC≌Rt△(　　)．

    　　⑤∵∠B＝∠，BC＝(已知)，

    　　∴Rt△ABC≌△Rt△(　　)．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    　　如图所示，在Rt△ABC中，AB=AC，∠BAC=90°，O为BC的中点．

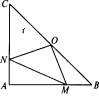
    　　①写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)；

     

    　　②如果点M、N分别在线段AB、AC上移动，在移动中保持AN=BM请判断△OMN的形状，并证明你的结论．

     

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书　九年级数学　上　（江苏版课标本） 江苏版课标本 题型：059

    利用切线性质证明等腰三角形

    　　如图，已知：如图(1)，AB是⊙O的直径，P是AB上的一点(与A、B不重合)．QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D，则△CDQ是等腰三角形．对上述命题证明如下：

    　　证明：连结OC．

    　　∵OA＝OC，∴∠A＝∠1．

    　　∵CD切⊙O于C点，

    　　∴∠OCD＝90°，

    　　∴∠1＋∠2＝90°，

    　　∴∠A＋∠2＝90°．

    　　在Rt△QPA中，∠QPA＝90°，

    　　∴∠A＋∠Q＝90°，

    　　∴∠2＝∠Q．∴DQ＝DC．

    　　即△CDQ是等腰三角形．

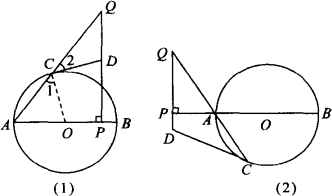
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图(2)所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案