
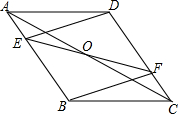
 如图所示,O为?ABCD对角线AC的中点,EF经过点O交AB于E,交CD于点F,连接DE、BF.求证:四边形EBFD为平行四边形.
如图所示,O为?ABCD对角线AC的中点,EF经过点O交AB于E,交CD于点F,连接DE、BF.求证:四边形EBFD为平行四边形. 分析 本题中要证明EBFD是平行四边形,已知DF∥BE,根据平行四边形的判定,我们可知只要证出DF=BE即可得出四边形EBFD是平行四边形,由于AB=DC,于是证AE=CF就是关键,那么就必须证得三角形AOE、OFC全等,这两个三角形中已知的条件有OA=OC,∠EAO=∠FOC,还有一组对顶角,因此就构成了全等三角形判定中的ASA,由此就可得出两三角形全等.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC.
∴∠EAO=∠FCO.
在△AOE与△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF,
∴AE=CF.
∵AB=CD,
∴(AB-AE)=(CD-CF),即DF∥BE,DF=BE,
∴四边形EBFD为平行四边形.
点评 本题考查了平行四边形的判定和全等三角形的判定等知识点,通过全等三角形来得出四边形的对边相等是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;
在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 时刻 | 12:00 | 13:00 | 16:00 |
| 碑上的数 | 是一个两位数 | 十位与个位数字与12:00时 所看到的正好颠倒了 | 比12:00时看到的两位数 中间多了个0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
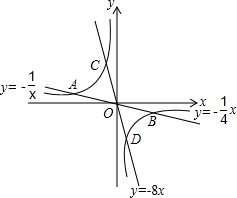 如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.
如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com