
 如图,一次函数y=kx+b的图象经过点A(0,2)和B(-3,0),则关于x的一元二次方程kx+b=0的解为x=-3.
如图,一次函数y=kx+b的图象经过点A(0,2)和B(-3,0),则关于x的一元二次方程kx+b=0的解为x=-3.  数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ⑤ | B. | ④⑤ | C. | ③④⑤ | D. | ①④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
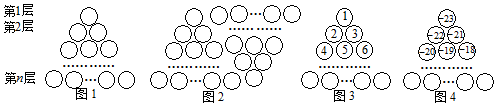
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
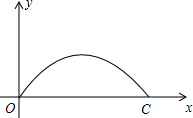 如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.
如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和24秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需32秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 12 | D. | 10$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com