
分析 已知等式为三个非负数的和为0的形式,只有这几个非负数都为0,可组成方程组,求x、y、z的值,即可求得3x+y-z的值.
解答 解:由非负数性质得:$\left\{\begin{array}{l}{x-2y-4=0}&{①}\\{2y+z=0}&{②}\\{x-4y+z=0}&{③}\end{array}\right.$,
①-③,得:2y-z=4 ④,
②+④,得:4y=4,解得:y=1,
将y=1代入②得:2+z=0,解得:z=-2,
将y=1代入①,得:x-2-4=0,解得:x=6,
∴3x+y-z=3×6+1-(-2)=21.
点评 考查了非负数的性质、三元一次方程组的解法,几个非负数的和为0时,这几个非负数都为0.


科目:初中数学 来源: 题型:解答题
 如图,已知直线y=kx-6与抛物线y=ax2+bx-3相交于A,B两点,且点A坐标为(1,-4),点B在x轴上.
如图,已知直线y=kx-6与抛物线y=ax2+bx-3相交于A,B两点,且点A坐标为(1,-4),点B在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=-$\frac{1}{2}$x+b与x轴、y轴分别交于点A、B,若点P(2,3)在△AOB内部,则b的可能值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴、y轴分别交于点A、B,若点P(2,3)在△AOB内部,则b的可能值是( )| A. | -3 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
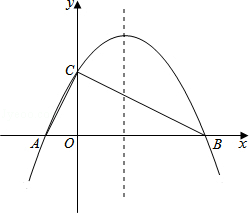 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.
如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
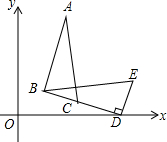 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com