解:(1)设直线AC的解析式为:y=kx+b,依题意,有:
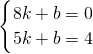
,解得
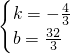
∴直线AC:y=-

x+
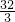
.
设抛物线的解析式为:y=ax
2+bx+c,依题意,有:
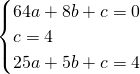
,解得
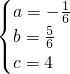
∴抛物线:y=-

x
2+

x+c.
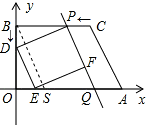
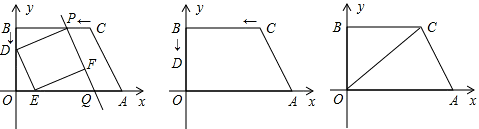
(2)过点B作BS∥AC,交x轴于点S,则AS=BC=5,OR=3,∴tan∠OBS=tan∠ODE=

.
BP=BC-CP=5-at=5-t,BD=t,OD=OB-BD=4-t,OE=

OD=3-

t;
由题意,四边形DEFP是平行四边形,若四边形DEFP是矩形,所以∠PDE=90°;
∵∠PDB=∠DEO=90°-∠ODE,∠PBD=∠DOE=90°,
∴△PBD∽△DOE,得
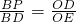
即:
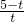
=

,解得 t=
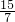
,则P(

,4);
由于直线PQ∥AC,设直线PQ:y=-

x+b,代入点P,得:
-

×

+b=4,解得 b=
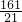
∴若a=1,当t=
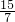
时,四边形DEFP为矩形;此时直线PQ的解析式:y=-

x+
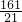
.
(3)同(2)可求得:△PBD≌△DOE,则 BD=OE,BP=OD;
∴
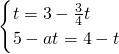
,解得
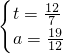
由题意,此时a的值不在0<a≤1.25的范围内,所以不存在符合条件的a、t值.
(4)易求得:直线OC:y=

x;直线AC:y=-

x+
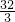
.
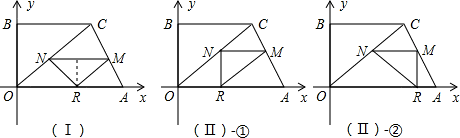
设点M、N的纵坐标为m,分两种情况讨论:
(Ⅰ)线段MN为等腰Rt△MNR的底边,则 MN=2m;
由MN∥OA,得:
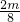
=
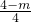
,解得 m=2;
∴M(
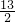
,2)、N(

,2)
∴点R(

,0).
(Ⅱ)线段MN为等腰Rt△MNR的腰,则 MN=m;
由MN∥OA,得:
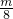
=
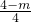
,解得 m=
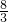
∴M(6,
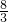
)、N(

,
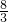
)
①当点N是直角顶点时,NR⊥x轴,点R(

,0);
②当点M是直角顶点时,MR⊥x轴,点R(6,0);
综上,存在符合条件的点R,且坐标为(

,0)、(

,0)、(6,0).
分析:(1)已知A、B、C三点的坐标,利用待定系数法能确定直线AC与抛物线的解析式.
(2)首先表示出BP、BD、OD、OE四边的长,若四边形DEFP为矩形,那么必须满足的条件是∠PDE是直角,此时△PBD、△DOE相似,可据此求出t的值,在求出BP的长以及点P的坐标后,利用待定系数法即可求出直线PQ的解析式(直线PQ与直线AC平行,那么它们的斜率相同,在设直线解析式时可利用这个特点).
(3)方法同(2),不过由四边形DEFP为正方形得出的条件变为△PBD、△DOE全等,首先由BD=OE求出t的值,再由OD=BP求出a的值;进一步能得到DP、DE的长,由此求得正方形的面积.
(4)此题需要注意两方面:
①线段MN是底边(此时线段MN的长是点M纵坐标的2倍);②线段MN为腰(此时线段MN的长等于点M的纵坐标);
解法大致相同,首先设出点M或N的纵坐标,利用△CMN、△CAO相似,求出这个纵坐标,再利用直线OC、直线AC解析式确定出点M、N的坐标后,即可得到点P的坐标.
点评:此题考查的是动点函数问题,主要涉及了利用待定系数法确定函数解析式、矩形和正方形的性质以及等腰直角三角形的判定和性质;其中还穿插了全等、相似三角形的性质以及解直角三角形的应用;综合性很强.在解答这道题时,对图示的理解很重要,着重体现了数形结合的重要性.

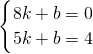 ,解得
,解得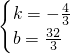
 x+
x+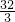 .
.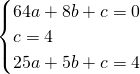 ,解得
,解得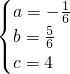
 x2+
x2+ x+c.
x+c. (2)过点B作BS∥AC,交x轴于点S,则AS=BC=5,OR=3,∴tan∠OBS=tan∠ODE=
(2)过点B作BS∥AC,交x轴于点S,则AS=BC=5,OR=3,∴tan∠OBS=tan∠ODE= .
. OD=3-
OD=3- t;
t;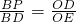
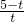 =
= ,解得 t=
,解得 t=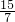 ,则P(
,则P( ,4);
,4); x+b,代入点P,得:
x+b,代入点P,得: ×
× +b=4,解得 b=
+b=4,解得 b=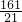
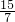 时,四边形DEFP为矩形;此时直线PQ的解析式:y=-
时,四边形DEFP为矩形;此时直线PQ的解析式:y=- x+
x+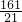 .
.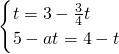 ,解得
,解得 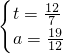
 x;直线AC:y=-
x;直线AC:y=- x+
x+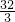 .
.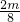 =
=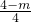 ,解得 m=2;
,解得 m=2;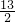 ,2)、N(
,2)、N( ,2)
,2) ,0).
,0).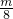 =
=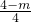 ,解得 m=
,解得 m=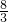
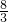 )、N(
)、N( ,
,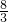 )
) ,0);
,0); ,0)、(
,0)、( ,0)、(6,0).
,0)、(6,0).


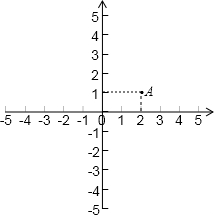 在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得△AOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,…,PK的坐标(有k个就标到PK为止,不必写出画法).
在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得△AOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,…,PK的坐标(有k个就标到PK为止,不必写出画法).