
【题目】如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,∠B=∠CFD. 证明:
(1)CF=EB
(2)AB=AF+2EB.
【答案】
(1)证明:∵AD是∠BAC的平分线,
∴∠CAD=∠DAE,
由已知有:∠ADC=90°﹣∠CAD,∠ADE=90°﹣∠DAE,
∴∠ADC=∠ADE,
在△ACD和△AED中
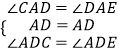
∴△ACD≌△AED(ASA),
∴CF=EB
(2)
证明:由(1)知FC=EB,AC=AE,
∴AB=AE+EB=AC+EB=AF+FC+EB=AF+2EB
【解析】(1)证明△ACD≌△AED即可;(2)由AB=AE+BE,结合条件可知AE=AC且BE=CF,代入可证得结论.
【考点精析】本题主要考查了角平分线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:初中数学 来源: 题型:
【题目】 (2016镇江)如图1,一次函数y=kx﹣3(k≠0)的图象与y轴交于点A,与反比例函数![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上的动点(于点A、B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求△OCD面积的最大值;
(3)将(2)中面积取得最大值的△OCD沿射线AB方向平移一定的距离,得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上(如图2),则点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于E. 
(1)若∠ABE=45°,求∠EBC的度数;
(2)若AB+BC=30,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1:△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)图中有几个等腰三角形?请说明EF与BE、CF间有怎样的关系. 
(2)若AB≠AC,其他条件不变,如图2,图中还有等腰三角形吗?如果有,请分别指出它们.另第(1)问中EF与BE、CF间的关系还存在吗?
(3)若△ABC中,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.如图3,这时图中还有哪几个等腰三角形?EF与BE、CF间的关系如何?为什么? 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com