
【题目】已知:如图,抛物线y ax2 - 2ax 3a交 x 轴正半轴于点 A,负半轴于点 B,交 y 轴于点C,tan∠OBC=3.
(1)求 a 值;
(2)点 P 为第一象限抛物线上一点,连接 AC、PA、PC,若点 P 的横坐标为 t, PAC 的面积为S,求 S与t的函数解析式,(请直接写出自变量 t 的取值范围);
(3)在(2)的条件下,过点 P 作 PD∥y 轴交 CA 延长线于点 D,连接 PB,交 y 轴于点 E,点 Q 为第二象限抛物线上一点,连接 QE 并延长分别交 x 轴、抛物线于点 N、F,连接 FD,交 x 轴于点 K ,当E 为 QF 的中点且 FN=FK 时,求直线 DF 的解析式.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() .
.
【解析】
(1)由抛物线![]() 与x轴相交,令
与x轴相交,令![]() ,求出
,求出![]() 、
、![]() ,再根据
,再根据![]() 求出点C的坐标,代入抛物线即可求出.
求出点C的坐标,代入抛物线即可求出.
(2)根据题意作图,过点P作![]() 轴分别交
轴分别交![]() 延长线、
延长线、![]() 轴于点
轴于点![]() ,过点C作
,过点C作![]() 交
交![]() 延长线于点H,得出点
延长线于点H,得出点![]() ,再解出直线AC的解析式和PN的代数式,运用三角形的面积公式即可求出 PAC的面积.
,再解出直线AC的解析式和PN的代数式,运用三角形的面积公式即可求出 PAC的面积.
(3)根据题意作图,延长PD交![]() 轴于点G,由题(2)可得
轴于点G,由题(2)可得![]() ,求出
,求出![]() ,得到
,得到![]() ,连接DE,得出四边形EOGD是矩形,再根据
,连接DE,得出四边形EOGD是矩形,再根据![]() ,得到
,得到![]() ,因而
,因而![]() ,再过点F作
,再过点F作![]() ,可得
,可得![]() .过点Q作
.过点Q作![]() 交RE延长线于点H,得到
交RE延长线于点H,得到![]() ,
,![]() ,
,![]() ,因而得出
,因而得出![]() ,再根据点F与点Q的坐标代数式,求得
,再根据点F与点Q的坐标代数式,求得![]() 、
、![]() ,即可求出直线DF解析式.
,即可求出直线DF解析式.
(1)解:∵抛物线![]() 与x轴相交,
与x轴相交,
∴令![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
(2)过点P作![]() 轴分别交
轴分别交![]() 延长线、
延长线、![]() 轴于点
轴于点![]() ,
,
过点C作![]() 交
交![]() 延长线于点H,点
延长线于点H,点![]() .
.
解出直线AC的解析式![]() ,
,
![]() ,
,
∴![]()
![]()
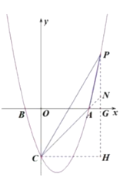
(3)延长PD交![]() 轴于点G,
轴于点G,![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,连接DE,
,连接DE,
∴四边形EOGD是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
过点F作![]() ,
,
∴![]() .
.
过点Q作![]() 交RE延长线于点H,
交RE延长线于点H,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() (舍),
(舍),
∴![]() ,
,![]() ,设直线DF的解析式为
,设直线DF的解析式为![]() ,
,
![]() ,
,![]() ,
,
∴直线DF解析式为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
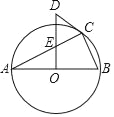
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
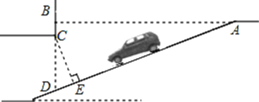
【题目】如图是某地下停车库入口的设计示意图,已知AB⊥BD,坡道AD的坡度i=1:2.4(指坡面的铅直高度BD与水平宽度AB的比),AB=7.2 m,点C在BD上,BC=0.4 m,CE⊥AD.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请根据以上数据,求出该地下停车库限高CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
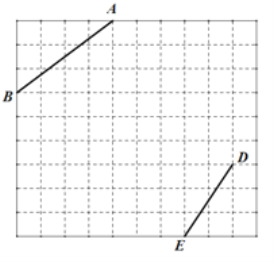
【题目】如图,方格纸中每个小正方形的边长均为 1,线段 AB、DE 的端点 A、B、D、E 均在小正方形的顶点上.
(1)在图中画一个以 AB 为一腰的等腰△ABC, 且tan ABC ![]() ,点C 在小正方形的顶点上;
,点C 在小正方形的顶点上;
(2)在图中画一个以 DE 为边的平行四边形 DEFG,且G 45° ,点 F、G 均在小正方形的顶点上,连接 CG,请直接写出线段 CG 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
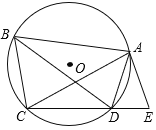
【题目】如图,四边形ABCD内接于⊙O,已知AB=AC,延长CD至点E,使CE=BD,连结AE.
(1)求证:AD平分∠BDE;
(2)若AB∥CD,求证:AE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,老百姓越来越依赖电商渠道获取必要的生活资料.小石经营的水果店也适时加入了某电商平台,并对销售的水果中的部分(如下表)进行促销:参与促销的水果免配送费且一次购买水果的总价满128元减![]() 元.每笔订单顾客网上支付成功后,小石会得到支付款的80%.
元.每笔订单顾客网上支付成功后,小石会得到支付款的80%.
参与促销水果 | |
水果 | 促销前单价 |
苹果 | 58元/箱 |
耙耙柑 | 70元/箱 |
车厘子 | 100元/箱 |
火龙果 | 48元/箱 |
(1)当![]() 时,某顾客一次购买苹果和车厘子各1箱,需要支付_____元,小石会得到______元;
时,某顾客一次购买苹果和车厘子各1箱,需要支付_____元,小石会得到______元;
(2)在促销活动中,为保障小石每笔订单所得到的金额不低于促销前总价的七折,则![]() 的最大值为_____.
的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.

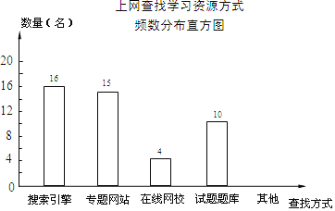
(1)频数分布表中![]() 的值:
的值:![]() _____________,
_____________,![]() ______________;
______________;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com