
����Ŀ��С���ͼ�λͬѧ���ֵ�Ӱ����Ϸʱ�����ֶ���ͬһ���壬Ӱ�ӵĴ�С���Դ������ľ����й�.��ˣ�������Ϊ�����Խ��������Ӱ�ӳ��ȼ����Դ�������λ��.���ǣ������������³���.
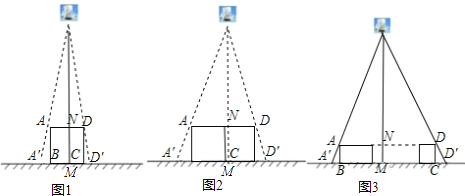
��1����ͼ1����ֱ�ڵ�����õ������ο��ABCD���߳�ABΪ30cm���������Ϸ���һ���ݣ��ڵ��ݵ������£������ο�ܵĺ���Ӱ��A��B��D��C�ij��Ⱥ�Ϊ6cm.��ô���������ĸ߶�Ϊ .
��2�����ı�ͼ1�е��ݵĸ߶ȣ��������߳�Ϊ30cm�������ο�ܰ�ͼ2�ڷţ�������ʱ����Ӱ��A��B��D��C�ij��Ⱥ�Ϊ���٣�
��3����n���߳�Ϊa�������ΰ�ͼ3�ڷţ���ú���Ӱ��A��B��D��C�ij��Ⱥ�Ϊb������������ľ���.��д��������̣�����ú�a��b��n�Ĵ���ʽ��ʾ��
���𰸡���1��x=180����2��y=12cm����3��![]()
��������
�����������1������ݵ�λ��Ϊ��P���á�PAD�ס�PA��D�䣬��������δ֪�����������������εĶ�Ӧ�ߵıȵ��ڶ�Ӧ�ߵıȣ��ɵõ��������ĸ߶ȣ�
��2��ͬ���ɵõ�����Ӱ��A��B��D��C�ij��Ⱥͣ�
��3��������Ӧ�����������ƣ��������������εĶ�Ӧ�ߵıȵ��ڶ�Ӧ�ߵıȣ�����ĸ��ʾ�������߶Σ����ɵõ����������ľ���.
�⣺��1������������ĸ߶�Ϊxcm��
��AD��A��D�䣬
���PAD=��PA��D�䣬��PDA=��PD��A��.
���PAD�ס�PA��D��.
�������������ζ�Ӧ�ߵıȵ������Ʊȵ����ʣ��ɵ�![]() ��
��
��![]() =
=![]() ��
��
���x=180.
��2�������Ӱ��A��B��D��C�ij��Ⱥ�Ϊycm��
ͬ���ɵá�![]() =
=![]() ��
��
���y=12cm��
��3���ǵ���Ϊ��P����ͼ��
��AD��A��D�䣬���PAD=��PA��D�䣬��PDA=��PD��A��.
���PAD�ס�PA��D��.
�������������ζ�Ӧ�ߵıȵ������Ʊȵ����ʣ��ɵ�![]()
��ֱ�ӵó����������ƻ�����߶ξ����۷֣�
�������������Ϊx�������⣬��PM=x��PN=x��a��AD=na��A��D��=na+b��
��![]() =1��
=1��![]()
![]() =1��
=1��![]()
x=![]()


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������˱���5��ͬѧ�ļ�ͥһ���µ�ƽ����ˮ������λ��t������¼���£�9��11��8��6��15�����������ݵ���λ����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
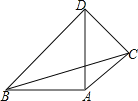
����Ŀ����һ�����ǰ尴��ͼ�����ڷ���һ������AC����tan��DACֵΪ�� ��
A.1
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A������Ϊ(1��0)����B������Ϊ(m��5��m)����AB�ij���Сʱ��m��ֵΪ_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�������ǣ� ��
A.���εĶԽ����ഹֱB.�Խ����ഹֱ���ı���������
C.���ε��ĸ��ڽǶ����D.�ĸ��ڽǶ���ȵ��ı����Ǿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
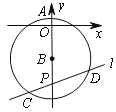
����Ŀ����ͼ��Բ����y��ĸ������ϣ��뾶Ϊ5�ġ�B��y��������ύ�ڵ�A��0��1��.����P��0����7����ֱ��l���B�ཻ��C��D���㣬����CD��������ֵ�������У� ��
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
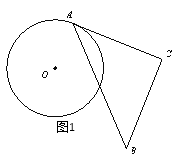
����Ŀ����һ�麬��45������ǰ�ABC�Ķ���A���ڡ�O�ϣ���AC���O�����ڵ�A����ͼ1��������ABC�ӵ�A��ʼ�����ŵ�A˳ʱ����ת������ת��Ϊ����0�㣼����135�㣩����ת��AC��AB�ֱ����O���ڵ�E��F������EF����ͼ2��.��֪AC=8����O�İ뾶Ϊ4.
��1������ת�����У������¼�����������EF�ij�����![]() �ij����ۡ�AFE�Ķ������ܵ�O��EF�ľ���.���в��������___________________������ţ���
�ij����ۡ�AFE�Ķ������ܵ�O��EF�ľ���.���в��������___________________������ţ���
��2��������________��ʱ��BC���O���У�ֱ��д���𰸣���
��3����BC���O����ʱ�����AEF�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
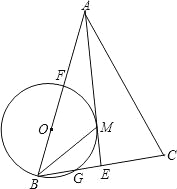
����Ŀ����֪��ͼ����ABC��AB=AC��AE�ǽ�ƽ���ߣ�BMƽ����ABC��AE�ڵ�M������B��M�������O��BC��G����AB�ڵ�F��FBǡΪ��O��ֱ����
��1����֤��AE����O���У�
��2����BC=6��cosC=![]() ������O��ֱ����
������O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѷ���ʽx2+ax+b�ֽ���ʽ���ã�x+1����x��3������a��b��ֵ�ֱ��ǣ� ��
A.a=2��b=3
B.a=��2��b=��3
C.a=��2��b=3
D.a=2��b=��3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com