Question

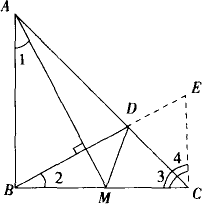
已知：如下图，△ABC中，∠ABC＝90°，AB＝BC，M是BC中点，D是AC上一点，BD⊥AM，求证：∠AMB＝∠DMC．

Answer 1

答案：
解析：

简证：作EC⊥BC与BD的延长线交于点E． 　　∵∠ABC＝90°，BD⊥AM， 　　∴∠1＝∠2， 　　∵AB＝BC，∠ABM＝∠BCE＝90°， 　　∴△ABM≌△BCE， 　　∴∠AMB＝∠E，BM＝CE＝CM， 　　又∠3＝∠4＝45°，CD为公共边， 　　∴△DMC≌△DEC， 　　∴∠DMC＝∠E， 　　∴∠AMB＝∠DMC． 　　分析：欲证角相等，通常通过三角形全等来实现．但图形本身不存在含∠AMB和∠DMC的两个全等的三角形．注意到AB＝BC及图形的特点，补全与△ABM全等的三角形，通过全等实现由已知向未知的转化． 　　简评：补全三角形构造全等，巧妙打开了解题的大门，问题变得“柳暗花明”．此题的其他解法略．