
分析 (1)由共有“一白三黑”4个围棋子,利用概率公式直接求解即可求得答案;
(2)首先画出树状图,然后由树状图求得所有等可能的结果与恰好提出“一黑一白”子的情况,然后利用概率公式求解即可求得答案
解答 解:(1)∵共有“一白三黑”4个围棋子,
∴P(黑子)=$\frac{3}{4}$;
(2)画树状图得: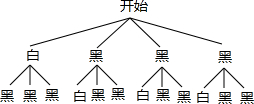
∵共有12种等可能的结果,恰好提出“一黑一白”子的有6种情况,
∴P(一黑一白)=$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题考查的是用列表法或树状图法求概率的知识.列表法或树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意此题是放回实验还是不放回实验是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com