练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
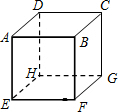
    15．用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH．若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的，而且共用了41个，大正方体其余部分用的都是表面均为白色的小正方体．则所用表面均为白色的小正方体共（　　）个．
    A．688B．959C．1290D．1687

    分析 根据四条对角线一共41个，也就是每条对角线都有11个小正方体（共用一个中心），所以大正方体的边长为小正方体的11倍，故一共需要11×11×11=1331个小正方体，再减去所需红色正方体，即得．

    解答 解：四条对角线一共41个，也就是每条对角线都有11个小正方体（共用一个中心），
    所以大正方体的边长为小正方体的11倍，
    故一共需要11×11×11=1331（个）小正方体，
    1331-41=1290（个）．
    故选C．

    点评 本题考查了认识立体图形，解决本题的关键是结合立体图形的特点解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年新疆乌鲁木齐市八年级下学期第一次月考数学试卷（解析版） 题型：填空题

    当x为________时，在实数范围内有意义.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省八年级3月月考数学试卷（解析版） 题型：判断题

    如图，在5×5的正方形网格中，每个小正方形的边长为1，请在所给网格中按下列要求画出图形.

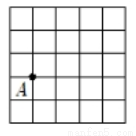
    （1）已知点A在格点（即小正方形的顶点）上，画一条线段AB，长度为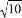，且点B在格点上.

    （2）以上题所画的线段AB为一边，另外两条边长分别为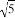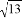，. 画一个△ABC，使点C在格点上（只需画出符合条件的一个三角形）.

    （3）所画出的△ABC的边AB上的高线长为 .（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知：A=$\frac{2002}{2003}$-$\frac{2001}{2002}$，B=$\frac{2001}{2002}$-$\frac{2000}{2001}$，则A＜B（选填“＞”“＜“或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知mn≠1且满足3m2-7m+1=0，n2-7n+3=0，则m-$\frac{m-1}{n}$的值为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知$\frac{1}{a}$$+\frac{1}{b}$=$\sqrt{3}（a≠b）$，求$\frac{a}{b（a-b）}-\frac{b}{a（a-b）}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．化简：$\frac{x}{x+2}-\frac{1}{x-1}÷\frac{x+2}{{x}^{2}-2x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．当m=-$\frac{1}{2}$，分式$\frac{{m}^{2}}{{m}^{2}+2m+1}$÷（1-$\frac{1}{m+1}$）=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．已知关于x的方程kx2+（1-k）x-1=0，下列说法正确的个数是（　　）
    A．当k=0时方程无解                   B．当k=1时方程有一个实数解
    C．当k=-1时方程有两个相等的实数解      D．当k≠1时方程总有两个不相等的实数解．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    同步练习册答案