
 已知:如图正方形ABCD,E是BC的中点,F在AB上,且BF=
已知:如图正方形ABCD,E是BC的中点,F在AB上,且BF= AB,猜想EF与DE的位置关系,并说明理由.
AB,猜想EF与DE的位置关系,并说明理由. AB,
AB, BC,
BC, EC,BE=
EC,BE= CD,
CD,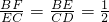 ,
, AB,即可证得
AB,即可证得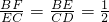 ,然后由两组对应边的比相等且夹角对应相等的两个三角形相似,即可证得△BEF∽△CDE,继而可求得∠DEF=90°,即可证得EF⊥DE.
,然后由两组对应边的比相等且夹角对应相等的两个三角形相似,即可证得△BEF∽△CDE,继而可求得∠DEF=90°,即可证得EF⊥DE.

科目:初中数学 来源: 题型:
 命题:一组邻边相等的矩形是正方形.
命题:一组邻边相等的矩形是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:标准大考卷·初中数学AB卷 九年级(上册) (课标华东师大版) (第3版) 课标华东师大版 第3版 题型:013
已知:如图,AB、CD是⊙O的两条直径,则四边形ADBC一定是

A.等腰梯形
B.正方形
C.菱形
D.矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com