
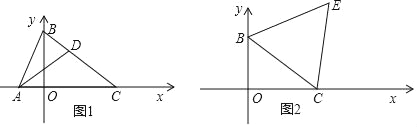
【题目】在平面直角坐标系xOy中,点B(0,3),点C(4,0)
(1)求线段BC的长.
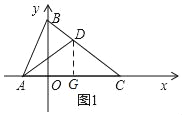
(2)如图1,点A(﹣1,0),D是线段BC上的一点,若△BAD∽△BCA时,求点D的坐标.
(3)如图2,以BC为边在第一象限内作等边△BCE,求点E的坐标.
【答案】(1)BC=5;(2)D(1.6,1.8);(3)点E的坐标为(2+![]() ,
,![]() ).
).
【解析】
(1)已知点B(0,3),点C(4,0),即可得到BO=3,CO=4,根据勾股定理求得BC=5;
(2)已知点A(﹣1,0),可得AO=1,得出AB2=AO2+BO2=10,再根据△BAD∽△BCA,即可得出AB2=BD×BC,求得BD=2,CD=3,过D作DG⊥AC于G,即可得DG∥BO,所以![]() ,由此可求得DG=1.8,CG=2.4,OG=1.6,即可得到D(1.6,1.8);(3)过E作EF⊥OC于F,EH⊥BO于H,设E(x,y),则EH=OF=x,EF=HO=y,得出HB=y﹣3,CF=x﹣4,依据勾股定理可得HE2+HB2=BE2=CE2=CF2+EF2,即x2+(y﹣3)2=25=(x﹣4)2+y2,进而得出点E的坐标.
,由此可求得DG=1.8,CG=2.4,OG=1.6,即可得到D(1.6,1.8);(3)过E作EF⊥OC于F,EH⊥BO于H,设E(x,y),则EH=OF=x,EF=HO=y,得出HB=y﹣3,CF=x﹣4,依据勾股定理可得HE2+HB2=BE2=CE2=CF2+EF2,即x2+(y﹣3)2=25=(x﹣4)2+y2,进而得出点E的坐标.
解:(1)如图1,∵点B(0,3),点C(4,0),
∴BO=3,CO=4,
∴BC=![]() =5;
=5;
(2)∵点A(﹣1,0),
∴AO=1,
∴AB2=AO2+BO2=10,
∵△BAD∽△BCA,
∴![]() =
=![]() ,即AB2=BD×BC,
,即AB2=BD×BC,
∴10=BD×5,
解得BD=2,
∴CD=3,
如图1,过D作DG⊥AC于G,则DG∥BO,
∴![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得DG=1.8,CG=2.4,
∴OG=1.6,
∴D(1.6,1.8);
(3)如图2,过E作EF⊥OC于F,EH⊥BO于H,
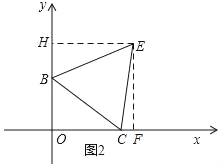
设E(x,y),则EH=OF=x,EF=HO=y,
∴HB=y﹣3,CF=x﹣4,
∵HE2+HB2=BE2=CE2=CF2+EF2,
即x2+(y﹣3)2=25=(x﹣4)2+y2,
解得x1=2+![]() ,x2=2﹣
,x2=2﹣![]() (舍去),
(舍去),
∴y=![]() +2
+2![]() ,
,
∴点E的坐标为(2+![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
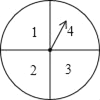
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线 x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)方程a(x﹣1)2 + b(x﹣1)+c=0的两根是x1= 0,x2= 6.其中正确的结论有( )
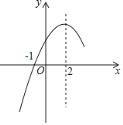
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程
有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c ;
是“倍根方程”,则c ;
(2)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值;
的值;
(3)若方程![]() 是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线
是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() 的根.
的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
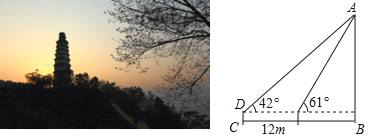
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,将线段BO绕点B顺时针旋转60°到BM,连接CM,OM.
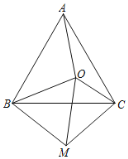
(1)求证:AO=CM;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
 【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
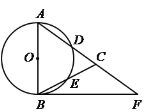
(1)求证:∠CBF=![]() ∠CAB. (2)若AB=5,sin∠CBF=
∠CAB. (2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
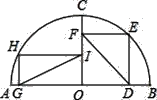
【题目】如图,C是以点O为圆心,AB为直径的半圆上一点,且CO⊥AB,在OC两侧分别作矩形OGHI和正方形ODEF,且点I,F在OC上,点H,E在半圆上,可证:IG=FD.小云发现连接图中已知点得到两条线段,便可证明IG=FD.
请回答:小云所作的两条线段分别是_____和_____;
证明IG=FD的依据是矩形的对角线相等,_____和等量代换.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com