
【题目】学校准备购置甲乙两种羽毛球拍若干,已知甲种球拍的单价比乙种球拍的单价多40元,且购买4副甲种球拍与购买6副乙种球拍的费用相同.
(1)两种球拍的单价各是多少元?
(2)若学校准备购买100副甲乙两种羽毛球拍,且购买甲种球拍的费用不少于乙种球拍费用的3倍,问购买多少副甲种球拍总费用最低?
【答案】
(1)解:设甲种球拍的单价为x元,乙种球拍的单价为(x﹣40)元,
根据题意得,4x=6(x﹣40),
解得:x=120,
x﹣40=80,
答:甲种球拍的单价为120元,乙种球拍的单价80元
(2)解:设购买m副甲种球拍总费用最低,总费用为y元,
根据题意得,120m≥3×80(100﹣m),
解得:m≥ ![]() ,
,
∵y=120m+80(100﹣m)=40m+8000
∵40>0,
∴当m取最小值时,总费用为y最小,
∴m=67时,总费用为y最小,
答:购买67副甲种球拍总费用最低
【解析】(1)设甲种球拍的单价为x元,乙种球拍的单价为(x﹣40)元,根据题意列方程即可得到结论;(2)设购买m副甲种球拍总费用最低,总费用为y元,根据题意列不等式得到m≥ ![]() ,根据函数的性质即可得到结论.
,根据函数的性质即可得到结论.


科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).下列结论:
①ac<0;
②4a﹣2b+c>0;
③抛物线与x轴的另一个交点是(4,0);
④点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2 . 其中正确的个数为( )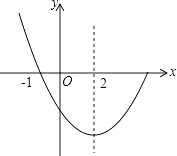
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() ABC中,AD平分
ABC中,AD平分 ![]() BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).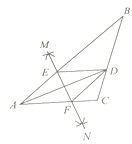
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(A2013防城港)如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下: 甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A.甲正确,乙错误
B.乙正确,甲错误
C.甲、乙均正确
D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.
(参考数据:sin22°≈ ![]() ,cos22°≈
,cos22°≈ ![]() ,tan22°≈
,tan22°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是CD的中点,AE是延长线交BC的延长线于F,分别连接AC,DF,解答下列问题: 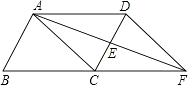
(1)求证:△ADE≌△FCE;
(2)若DC平分∠ADF,试确定四边形ACFD是什么特殊四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com