

 m
m
 x,
x, m.
m. m.
m.

科目:初中数学 来源:不详 题型:解答题
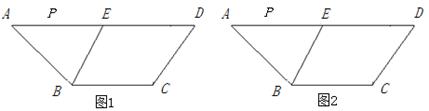
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
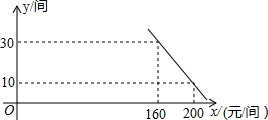
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
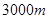 的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加
的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加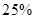 ,结果提前
,结果提前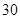 天完成这一任务,实际每天铺设多长管道?
天完成这一任务,实际每天铺设多长管道?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
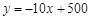 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com